Решение комбинаторных задач - Перебор возможных вариантов - Натуральные числа

Цель: сформировать навыки решения комбинаторных задач с помощью построения графов.

Ход урока

I. Организационный момент.

II. Устная работа.

1. Наташа сшила кукле 10 разных платьев, а Даша сшила своему мишке 3 штанишек и 4 футболки. У кого больше разных нарядов — у куклы или у мишки?

2. Служитель зоопарка должен дать зайцу 2 различных овоща. Сколькими способами он может это сделать, если у него есть морковь, свекла и капуста?

III. Проверка домашнего задания.

У, № 169, 171, 175.

IV. Формирование умений и навыков.

1. Фронтальная работа с классом по решению задач.

Задача 1. Женя, Дима, Максим и Алеша сыграли между собой по одной партии в шахматы. Сколько всего партий было сыграно?

Задача 2. Вася, Коля, Петя, Аня и Наташа — лучшие лыжники в 5 классе. Для участия в соревнованиях нужно выбрать одного мальчика и одну девочку. Сколькими способами это можно сделать?

1. Обсуждение задач.

а) К какому разделу математики относится первая задача?

б) Относится ли к комбинаторным вторая задача? Объясните свой ответ.

2. Рассмотрим два способа решения задачи 1.

Способ 1. Женя сыграл партию с Димой, партию с Максимом, партию с Алешей. Дима также сыграл три партии — с Женей, Максимом и Алешей. Но партию Димы с Женей мы уже посчитали. Остается добавить одну партию, которую сыграли Максим с Алешей. Поэтому искомое число партий равно 3 + 2 + 1 = 6.

ЖД, ЖМ, Ж.

ДМ, ДА

МА

Способ 2. Каждая линия обозначает сыгранную партию. Всего на схеме 6 линий, значит, всего сыграно 6 партий (рис. 38).

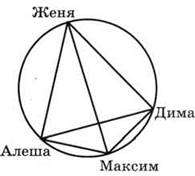
Рис. 38

Какое решение вам понравилось больше? Почему?

3. Схема решения задачи во втором способе называется ГРАФ (это слово происходит от греческого «графо» — пишу). Граф состоит из вершин и ребер. Подумайте, где у данного графа вершины и где ребра. Что обозначают вершины? Что обозначают ребра?

4. Попробуйте решить вторую задачу при помощи графа. Если построить граф к этой задаче вы не смогли, подумайте, какой из графов мог бы к ней подойти (рис. 39).

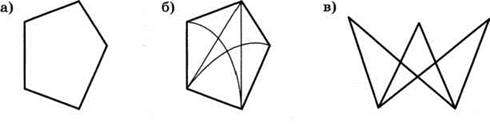
Рис. 39

2. Работа в группах.

Группа 1.

1. Прочитайте задачи.

а) В киоске продаются шоколадки стоимостью 3 р. и мороженое стоимостью 2 р. 50 к. Таня купила несколько шоколадок и несколько мороженых и заплатила за все 13 р. 50 к. Сколько мороженых и сколько шоколадок купила Таня?

б) В магазине продаются 3 вида шоколадок и 4 сорта мороженого. Дима хочет купить шоколадку и мороженое. Сколькими способами он может сделать покупку?

2. Есть ли среди них комбинаторная задача? Если есть, то какая? Как это узнать?

3. К какой из задач может относиться такой граф (рис. 40)?

Объясните, как он построен.

Что могут обозначать буквы у его вершин, что обозначают ребра?

Этот граф построен полностью? Если нет, завершите его построение.

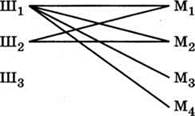
Рис. 40

Группа 2.

1. Найдите среди задач комбинаторные.

а) Пятеро ученых, участвовавших в научной конференции, обменялись рукопожатиями. Сколько всего рукопожатий было сделано?

б) Самому молодому из этих ученых 28 лет, самому старшему — 63 года, всем пятерым вместе 197 лет. Найдите возраст остальных участников конференции, если известно, что каждому из них больше 34 лет.

в) На прощание эти ученые обменялись визитными карточками. Сколько всего карточек было передано из рук в руки?

2. Постройте к комбинаторным задачам графы и решите их.

3. Если затрудняетесь, подумайте, правильно ли вы начали строить к этим задачам графы. К какой из комбинаторных задач относится каждый из графов (рис. 41)?

Рис. 41

4. Сравните число рукопожатий и число визитных карточек. Ответ объясните.

Группа 3.

1. Вершины графа (рис. 42) обозначают населенные пункты, ребра — дороги. Сколькими способами можно выбрать маршрут из А в С?

2. Сколькими способами можно доехать из А в С, а затем вернуться обратно, если нельзя дважды проезжать по одной и той же дороге? А если можно?

3. Измените граф так, чтобы он стал сложнее. Составьте к новому графу новую комбинаторную задачу.

Группа 4.

1. Прочитайте задачу и попробуйте составить к ней граф. Саша, Петя и Коля собираются сесть в трехместную байдарку и думают, кому из них сесть спереди, кому посередине, а кому на корме. Сколькими способами мальчики могут разместиться в байдарке?

2. В комбинаторике есть много задач, которые удобно решать с помощью графов, но часто встречаются и такие, которые решаются другими способами. Решите данную задачу другим способом.

3. Если затрудняетесь, рассмотрите такую схему (рис. 43). Объясните, какое отношение она имеет к задаче. Какие схемы еще можно составить?

Что получим, если эти схемы объединим? (Дерево возможных вариантов.)

Рис. 42

Рис. 43

3. Обсуждение работ, представленных каждой группой.

4. Самостоятельное решение задачи.

Из Дома отдыха на стадион ведут три различные дороги и от стадиона до озера тоже три дороги. Отдыхающие обычно после тренировки на стадионе идут купаться на озеро. Могут ли 8 отдыхающих дойти от Дома отдыха до озера с заходом на стадион разными маршрутами?

V. Итоги урока.

1. Назовите элементы, из которых состоит граф.

2. Что обозначают вершины графа?

3. Что обозначают ребра графа?

VI. Домашнее задание.

У, № 165, 166, 174. Решите задачи разными способами.