Экстремумы функций нескольких переменных - ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Определение. Точка M0(x0, у0) называется точкой максимума функции z = f(x, у), если существует некоторая окрестность точки M0(x0, у0), для всех точек М(х, у) которой выполняется неравенство f(x0, у0) ≥ f(x, у).

Точка М0(х0, у0) называется точкой минимума функции z = f(x, у), если существует некоторая окрестность точки M0(x0, у0), для всех точек M(x, у) которой выполняется неравенство f(x0, у0) ≤ f(x, у).

Необходимое условие экстремума. Если M0(x0, у0) является точкой экстремума функции z = f(x, у) и если в этой точке существуют частные производные функции, то они равны нулю

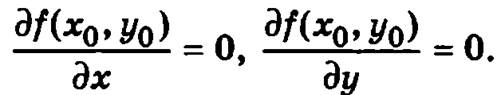
Определение. Точка, в которой частные производные функции z = f(x, у) первого порядка равны нулю, называется стационарной точкой функции.

Достаточные условия экстремума. Если функция z = f(x, у) определена и имеет непрерывные частные производные второго порядка в некоторой окрестности стационарной точки М0(х0,y0), то при 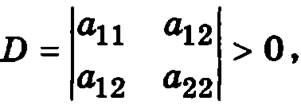где 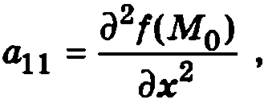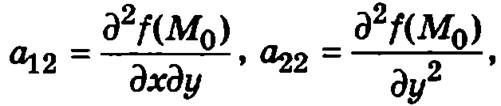точка M0(x0, y0) является точкой минимума при а11 > 0 и точкой максимума при a11 < 0 при D < 0 точка М0(x0, у0) не является точкой экстремума, а при D = 0 установить наличие экстремума функции в точке М0(x0, у0) невозможно и для этого необходимо проводить более детальное исследование с привлечением частных производных более высокого порядка.

Пример. Найдем экстремумы функции

Найдем стационарные точки данной функции:

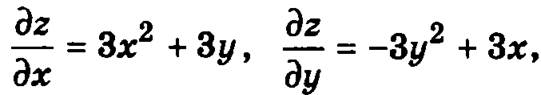
тогда стационарные точки определим из системы уравнений:

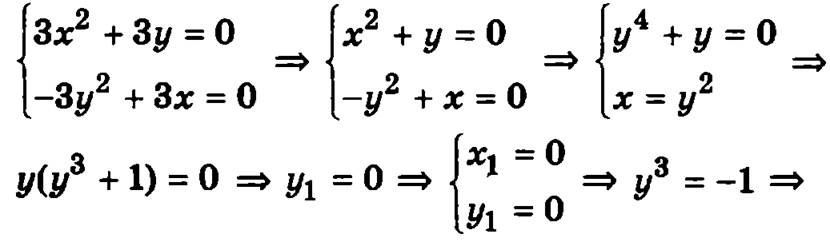
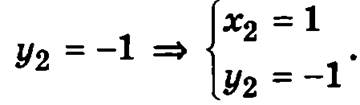
Таким образом функция имеет две стационарные точки M1(0, 0) и М2(1, -1), исследуем каждую из них:

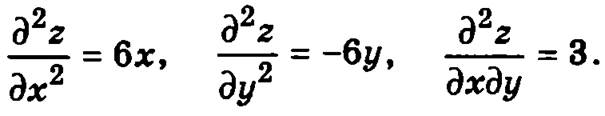
Для точки М1(0, 0):

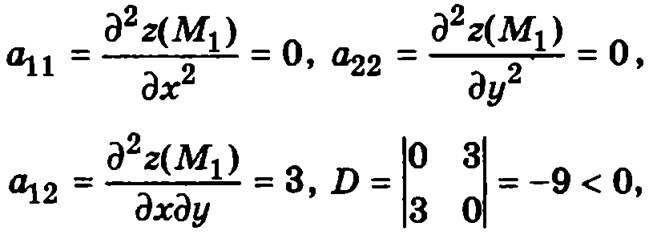
следовательно, в точке М1(0, 0) функция экстремума не имеет.

Для точки М1(1, -1):

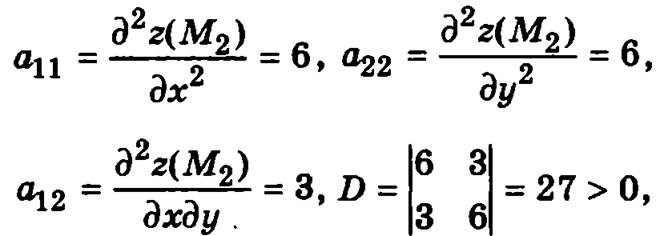
следовательно, в точке М1(0, 0) функция имеет экстремум, и, так как а11 > 0, этот экстремум — минимум.

Таким образом zmin = z(M2) = 4.