Частные производные высших порядков - ФУНКЦИИ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ

Допустим, что функция z = f(x, у) определена в области D и имеет в этой области частные производные dz/dx и dz/dy, которые тоже являются функцией переменных и которые тоже могут иметь частные производные. Частные производные от частных производных функции называются частными производными второго порядка:

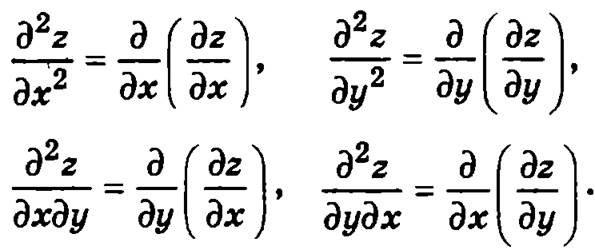
Частные производные второго порядка, которые получаются дифференцированием функции по разным аргументам 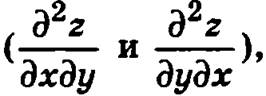называются смешанными.

Теорема. Если функция z = f(x, у) определена в области D и имеет в этой области непрерывные вторые смешанные частные производные 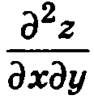и 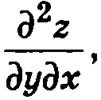то справедливо равенство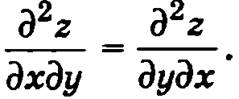

По аналогии с частными производными второго порядка можно определить частные производные более высоких порядков.

Также можно определить дифференциалы функции более высоких порядков, например, дифференциал второго порядка: