Высшая математика мини-справочник для ВУЗов
Прямая в пространстве - АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ
Каноническое уравнение прямой:
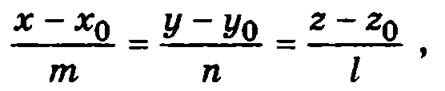
где M0(x0, y0, z0) — точка, лежащая на этой прямой, ![]() — направляющий вектор прямой.
— направляющий вектор прямой.
Уравнение прямой, проходящей через две заданные точки М0(x0, y0, z0) и M1(x1, y1, z1):
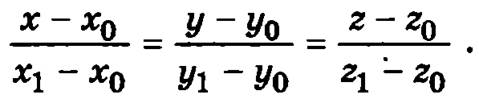
Параметрическое уравнение прямой в пространстве:
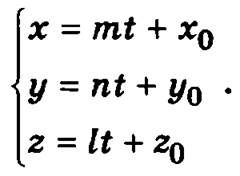
Векторное уравнение прямой в пространстве:
![]()
где ![]() — радиус-вектор текущей точки прямой М(х, у, z),
— радиус-вектор текущей точки прямой М(х, у, z), ![]() — радиус-вектор точки прямой M0(x0, y0, z0), t — параметр, каждому значению которого соответствует некоторая точка прямой (-∞ < t < +∞).
— радиус-вектор точки прямой M0(x0, y0, z0), t — параметр, каждому значению которого соответствует некоторая точка прямой (-∞ < t < +∞).
Пусть заданы канонические уравнения двух пересекающихся прямых
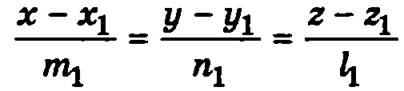
и
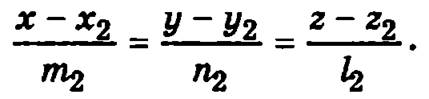
Тогда угол φ между этими прямыми определяется из соотношения
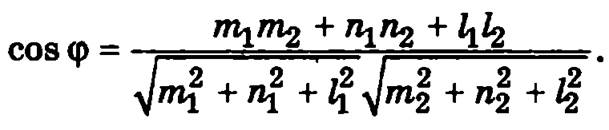
Прямые будут параллельны, если
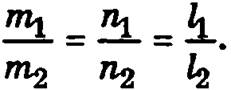
Прямые будут перпендикулярны, если
![]()
Пусть заданы уравнения плоскости Ах + By + Cz + D = 0 и каноническое уравнение прямой 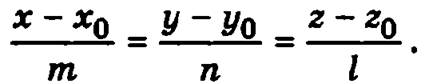 Тогда угол φ между прямой и плоскостью определяется из соотношения
Тогда угол φ между прямой и плоскостью определяется из соотношения
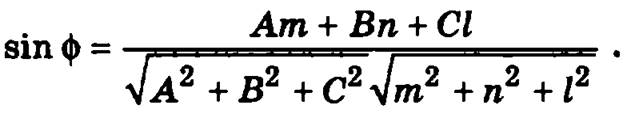
Если выполняется соотношение Аm + Вn + Сl = 0, то прямая параллельна плоскости.
Если выполняется соотношение ![]() то прямая перпендикулярна плоскости.
то прямая перпендикулярна плоскости.