Математика 9 класс подготовка к ГИА
Вариант № 30 - Учебно-тренировочные тесты
Вариант № 30
Часть 1
Модуль «Алгебра»
1. Найдите среднее арифметическое чисел 1,23; —2,5 и 0,1.
Ответ: _____________ .
2. Выберите обыкновенную дробь, равную десятичной периодической дроби 4,4(3).
![]()
3. Какое из следующих неравенств не следует из неравенства с > b – a?

4. Решите уравнение ![]()
Ответ: _____________ .
5. Сколько надо взять первых подряд идущих членов арифметической прогрессии 5, 9, 13, ..., чтобы получить в сумме 230?
Ответ: _____________ .
6. Какая из следующих функций может описывать параболу, изображённую на рисунке 225?
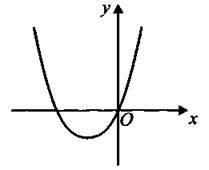
Рис. 225

7. Какой из следующих квадратных трёхчленов нельзя разложить на линейные множители?

8. Найдите наибольшее целое х, удовлетворяющее неравенству ![]()
Ответ: _____________ .
Модуль «Геометрия»
9. Биссектриса внешнего угла равнобедренного треугольника АВС при основании АС образует с основанием угол, величина которого равна 126°. Найдите величину угла АВС. Ответ дайте в градусах.
Ответ: _____________ .
10. Хорда, длина которой равна 7√12, стягивает дугу, величина которой равна 120°. Найдите радиус окружности.
Ответ: _____________ .
11. Найдите площадь прямоугольника, если его диагональ равна 3√41, а одна из его сторон равна 15.
Ответ: _____________ .
12. На клетчатой бумаге с клетками размером 1 см х 1 см изображена трапеция (см. рис. 226). Найдите её площадь в см2.
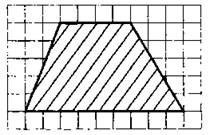
Рис. 226
Ответ: _____________ .
13. Укажите в ответе номера верных утверждений.
1) Если угол равнобедренного треугольника равен 50°, то его основание больше боковой стороны.
2) Треугольник со сторонами 5√3 см, 5 см и 10 см является прямоугольным.
3) Биссектрисы углов параллелограмма, прилежащих к одной стороне, пересекаются под прямым углом.
4) Площадь треугольника равна половине произведения двух любых его сторон на синус угла между ними.
Ответ: _____________ .
Модуль «Реальная математика»
14. Из пункта А в пункт В, расстояние между которыми 21 км, выехали одновременно мотоциклист со скоростью 14 м/с и велосипедист со скоростью 10 м/с. На сколько минут раньше в пункт В попадёт мотоциклист?
15. Ученик вычислил значения некоторой линейной функции у(х) = ax + b:
|
x |
-2 |
-1 |
0 |
1 |
2 |
|
y |
-1 |
1 |
3 |
4 |
7 |
Известно, что при вычислении ровно одного из значений этой функции ученик ошибся. Какое из значений найдено неверно?
1) y(1.
2) y(2.
3) y(—1.
4) y(0)
16. К 100 г 20%-ного раствора соли добавили 300 г её 10%-ного раствора. Найдите концентрацию полученного раствора (в процентах).
Ответ: _____________ .
17. В ясный солнечный день требуется измерить высоту АВ дерева (см. рис. 227). При этом ВС = 14 м — длина тени, отбрасываемой деревом; DE = 2 м — длина вертикального шеста; ЕК = 2,5 м — длина тени, отбрасываемой шестом. Найдите высоту дерева в метрах.
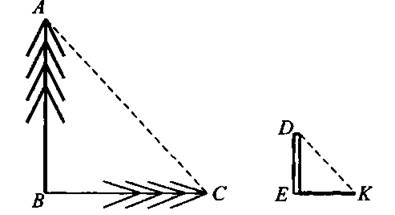
Рис. 227
Ответ: _____________ .
18. В фермерском хозяйстве площади, отведённые под посевы зерновых, распределены, как показано на круговой диаграмме (см. ниже рис. 228). Какое из утверждений относительно представленных данных является неверным, если общая площадь земли, отведённой под посевы зерновых, равна 150 га?
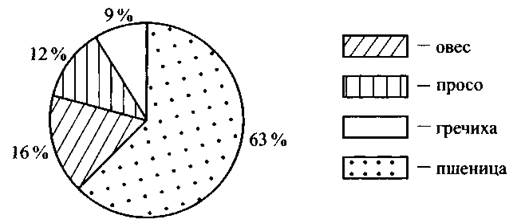
Рис. 228
1) Площадь, отведённая под посев овса, равна 24 га.
2) Суммарная площадь, отведённая под посевы овса, проса и гречихи, составляет 70 га.
3) Более половины всей посевной земли занято пшеницей.
4) Посевы гречихи и проса занимают примерно пятую часть всей посевной земли.
19. В коллекции 200 монет, из которых 25 монет XVIII века. Какова вероятность того, что наудачу выбранная монета датирована XVIII веком?
Ответ: _____________ .
20. Высота h(t) полёта снаряда (до его падения), выпущенного из артиллерийского орудия, описывается формулой h(t) = -5t2 + 36t, где t — время в секундах, прошедшее с момента выстрела, h(t) измеряется в метрах. Вычислите, сколько секунд снаряд находился на высоте не менее 7 м.
Ответ: _____________ .
Часть 2
Задания этой части выполняйте с записью решения
Модуль «Алгебра»
21. Решите неравенство ![]()
22. Поезд должен был пройти 1680 км за определённое время. На половине пути он был задержан у семафора на 1 ч и, для того чтобы прибыть к месту назначения в срок, увеличил скорость на 4 км/ч. Сколько часов (включая время стоянки) поезд находился в пути?
23. Постройте график функции 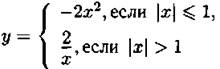 и определите, при каких значениях m прямая у = 4m будет иметь с графиком единственную общую точку.
и определите, при каких значениях m прямая у = 4m будет иметь с графиком единственную общую точку.
Модуль «Геометрия»
24. Трапеция, средняя линия которой равна √3/3, равновелика равностороннему треугольнику со стороной 11. Найдите высоту трапеции.
25. Даны три точки: A(2; 1), В(8; 3), (7(5; 2). Докажите, что эти точки лежат на одной прямой.
26. В ромбе ABCD биссектриса угла ACD делит сторону AD пополам. Найдите углы ромба.