Математика 9 класс подготовка к ГИА
Решение варианта № 5 - Учебно-тренировочные тесты
Решение варианта № 5
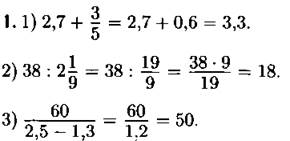
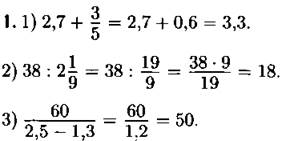
Ответ: 3.
2. Заметим, что a < 0 и b > 0 (см. рис. 33).
1) Утверждение b - a < 0 — неверно, так как разность положительного и отрицательного чисел положительна.
2) Утверждение a/b > 0 — неверно, так как a < 0, b > 0, дробь a/b отрицательна.
3) Утверждение |b| < |а| — неверно. Из рисунка видно, что расстояние от точки b до начала координат больше расстояния от точки а до начала координат, то есть |b| > |а|.
4) Утверждение а < 1/b < 1 — верно, так как 0 < 1/b < 1, a — число отрицательное.
Ответ: 4.
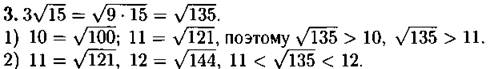
Таким образом, 11 < 3√15 < 12. Так как √135 < 12, то пункты 3 и 4 не подходят.
Ответ: 2.
4. Решим уравнение 4х2 + 8х - 5 = 0, найдя дискриминант:
D = 82 - 4 ∙ 4 ∙ (-5) = 64 + 80 = 144.
D > 0, поэтому исходное уравнение имеет два различных корня:
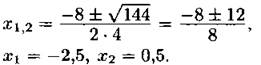
Ответ: —2,5; 0,5.
5. На рисунке А изображён график функции 1) у = 2х — 1 — это прямая, проходящая через точки х = 0, у = -1; х = 1, у = 1.
На рисунке Б изображён график функции 3) у = —2х + 1, это прямая, проходящая через точки х = 0, у = 1; х = 1, у = -1.
На рисунке В изображён график функции 2) у = 2х + 1, это прямая, проходящая через точки x = 0, у = 1; x = 1, у = 3.
Ответ: 132.
6. 1) Внесём «минус» в первый сомножитель, получим —(а — 3)(2 — 3а) = (3 — а)(2 — 3а), то есть представленное первое равенство неверно.
2) (5 — а)(а + 5) = (5 — а)(5 + а) = 25 — а2, то есть представленное второе равенство верное.
3) (a — 6)2 = а2 — 12а + 36.
Отсюда делаем вывод, что представленное равенство неверное.
4) —(7 + а)(2а — 3) = (7 + а)(3 — 2а) = 21 — 11а — 2а2, то есть получили выражение, равное представленному в задании. Значит, равенство верное.
Ответ: 24.
7. Упростим выражение: ![]()
Найдём значение при х = -0,3, у = 1,2.
![]()
Ответ: —3.
8. Решим уравнение: ![]()
Ответ: 0,2.
9. 1) ∆MNK ~ ∆LFK (по первому признаку подобия треугольников, ∠K — общий, ∠MNK = ∠LFK — соответственные углы при параллельных прямых MN и LF и секущей NK).
![]()
Ответ: 24.
10. Меньшая диагональ ромба находится напротив меньшего угла, который равен 180° — 120° = 60° (см. рис. 229).
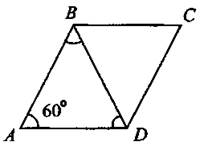
Рис. 229
Так как АВ = AD, то ∆ABD — равнобедренный и ∠ABD = ∠ADB = 60°. ∆ABD — равносторонний, BD = AD = АВ = 30.
Ответ: 30.
11. Обозначим площадь оставшейся части S (см. рис. 230). S = Sabcd — Saefk. S = 102 — 6 ∙ 4 = 76 (см2).
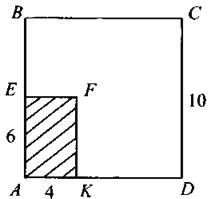
Рис. 230
Ответ: 76.
12. Используя теорему о касательной и секущей, записываем равенство К А ∙ КВ = KL2 (см. рис. 231).
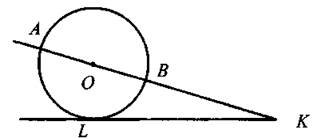
Рис. 231
К А = КО + ОА = 10 + 6 = 16 см.
КВ = КО - ОВ, КВ = 10 - 6, КВ = 4 см.
KL2 = 16 ∙ 4, KL = 8 см.
Ответ: 8.
13. Рассмотрим каждое из предложенных утверждений.
Утверждение 1) верно, так как ромб является параллелограммом, диагонали ромба взаимно перпендикулярны.
Утверждение 2) неверно, так как условия, что два угла одного треугольника соответственно равны двум углам другого, недостаточно, чтобы треугольники были равны.
Утверждение 3) верно (на основании признака равенства треугольников).
Ответ: 13.
14. Найдём время, которое затратил велосипедист на прохождение пути в 40 км — это 40/25 = 1,6 (ч) и в 30 км — 30/20 = 1,5 (ч).
Таким образом, общее время равно 1,6 + 1,5 = 3,1 (ч).
Ответ: 3,1.
15. По графику определяем, что цена деления по горизонтальной оси — 5 мин, цена деления по вертикальной оси равна 10 °С.
Далее определяем, что 10 °С соответствует 10 минутам, а 80 °С соответствует 35 минутам.
35 — 10 = 25 (мин) — занял процесс нагревания с 10 °С до 80 °С.
Ответ: 25.
16. Площадь участка равна 10 ар, и она распределена на 5 частей (4 + 1), из которых 4 части занимает фруктовый сад. То есть площадь сада равна 10 : 5 ∙ 4 = 8 (ар).
Ответ: 8.
17. Сечение гайки имеет 6 осей симметрии (см. рис. 232).
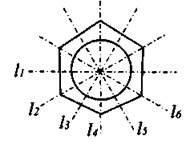
Рис. 232
Ответ: 6.
18. Используя диаграмму, находим количество месяцев, средняя температура воздуха в которых выше 20 °С. Это месяцы 6, 7, 8, 9.
Ответ: 4.
19. Всего ручек 8 + 12 = 20 (штук). С синей пастой — 8 штук. Вероятность того, что Вася возьмёт наугад ручку с синей пастой, равна 8/20.
![]()
Ответ: 0,4.
20. Найдём вес тела подстановкой исходных данных m = 40 кг, g = 9,8 м/с2, a = 1,4 м/с2 в формулу р = m(g + а). Тогда р = 40(9,8+1,4), р = 40 ∙ 11,2, р = 448 Н.
Ответ: 448.
21. Исходное неравенство равносильно неравенству 4х2 — 5x — 21 ≤ 0.
Решим уравнение 4х2 - 5х - 21 = 0, его корни х1 = —7/4 и х2 = 3, откуда ![]()
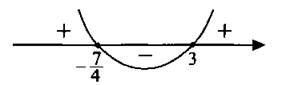
Рис. 233
По рисунку 233 находим решение: х ∈ (-7/4; 3).
Ответ: (-7/4; 3).
22. 3х2 — 15х + 2m = 0, x1 = 2.
Подставим в уравнение значение х = 2 и найдём m:
3 ∙ 22 - 15 ∙ 2 + 2m = 0,
12 — 30 + 2m = 0, 2m = 18, m = 9.
Ответ: 9.
23. Ровно одну общую точку прямая у = сх — 9 и парабола у — х2 + 5х будут иметь в том случае, когда уравнение сх — 9 = х2 + 5х будет иметь ровно один корень.
х2 + (5 - с)х + 9 = 0. Дискриминант квадратного трёхчлена должен быть равен нулю.
(5 - с)2 - 4 ∙ 9 = 0,
25 - 10с + с2 - 36 = 0,
с2 — 10с — 11 = 0, откуда c1 = —1, c2 = 11. Отрицательным является только c1 = —1, при котором уравнение принимает вид х2 + 6х + 9 = 0, откуда х = —3. Тогда у = (—3)2 + 5 ∙ (-3) = —6.
Построим графики прямой у = —х — 9, параболы у = х2 + 5х. Прямую у = —х — 9 построим по точкам (—9: 0) и (0; -9). Вершина параболы у = х2 + 5х находится в точке (—2,5; —6,25), ветви направлены вверх, координатные оси парабола пересекает в точках (—5; 0) и (0; 0) (см. рис. 234).

Рис. 234
Ответ: с = —1, (—3: — 6).
24. По условию ∠BAD = 46° и ∠CBD = 33°, требуется найти величину угла ABD. Так как ABCD — параллелограмм по условию, то противоположные стороны ВС и AD параллельны.
∠BDA = ∠CBD как внутренние накрест лежащие углы при параллельных прямых AD и ВС и секущей BD. Следовательно, ∠BDA = 33°.
∠ABD = 180° - (∠BAD + ∠ADВ) = 180° - (46° + 33°) = 180° - 79° = 101°.
Ответ: 101°.
25. По условию (см. рис. 235) KF ⊥ FT и LT ⊥ FT, следовательно KF || LT. А так как KF = LT по условию, то четырёхугольник KLTF — параллелограмм (по первому признаку параллелограмма). Делаем вывод: KL || FT как противоположные стороны параллелограмма. Таким образом, ∠ОКL = ∠OTF как накрест лежащие углы при параллельных прямых KL и FT и секущей КТ, что и требовалось доказать.
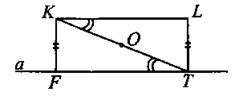
Рис. 235
26. По условию (см. рис. 236) СА и СН — касательные к окружности с центром в точке О, СО — биссектриса угла АСН, СО1 — биссектриса угла ИСК. Углы АСН и НСК — смежные. По свойству биссектрис смежных углов ∠ОСО1 = 90°. Центры окружностей лежат на биссектрисе ∠ВАС, поэтому OO1 ⊥ ВС, СН — высота ∆ОСО1. В прямоугольном треугольнике ОСО1 по свойству высоты, проведённой из вершины прямого угла к гипотенузе, имеем СН2 = ОН ∙ O1Н.
62 = 4,5 ∙ О1H,
![]()
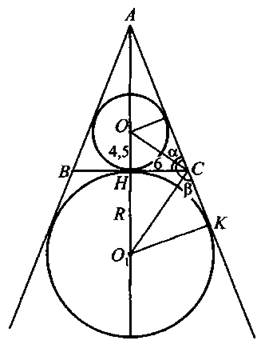
Рис. 236
Ответ: 8 см.