Математика 9 класс подготовка к ГИА
Вариант № 5 - Учебно-тренировочные тесты
Вариант № 5
Часть 1
Модуль «Алгебра»
1. Найдите значения выражений. В ответе укажите номер наибольшего из найденных значений.
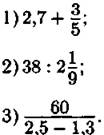
Ответ: _________________.
2. Выберите верное утверждение относительно чисел а и b, расположенных на числовой прямой (см. рис. 33).
![]()
Рис. 33
![]()
3. Укажите два соседних целых числа, между которыми заключено число 3√15.
1) 10 и 1.
2) 11 и 1.
3) 12 и 1.
4) 13 и 14
4. Найдите корни уравнения 4х2 + 8x - 5 = 0.
Ответ: _________________.
5. На рисунке 34 изображены графики трёх функций, задаваемых формулами вида у = kх + b. Укажите для каждого графика соответствующую ему формулу, выбрав её из числа приведённых ниже.
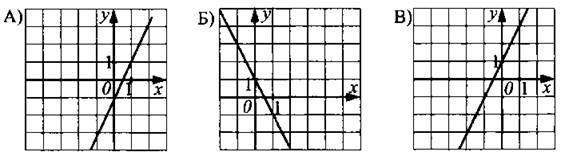
Рис. 34
1) у = 2х — .
2) у = 2x + .
3) у = —2х + .
4) у = —2х — 1
Ответ: 
6. Запишите в ответе номера верных равенств.
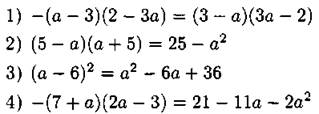
Ответ: _________________.
7. Упростите выражение ![]() и найдите его значение при х = -0,3, у = 1,2.
и найдите его значение при х = -0,3, у = 1,2.
Ответ: _________________.
8. Решите уравнение ![]()
Ответ: _________________.
Модуль «Геометрия»
9. Периметр равностороннего треугольника MNK равен 48, LF — средняя линия. Найдите периметр треугольника LFK (см. рис. 35).
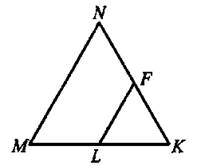
Рис. 35
Ответ: _________________.
10. Сторона ромба равна 30, а тупой угол равен 120° (см. рис. 36). Найдите длину меньшей диагонали ромба.
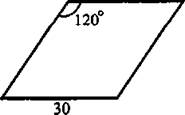
Рис. 36
Ответ: _________________.
11. Из квадрата со стороной 10 см вырезали прямоугольник со сторонами 4 см и 6 см (см. рис. 37). Найдите площадь оставшейся части. Ответ дайте в см2.
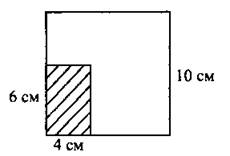
Рис. 37
Ответ: _________________.
12. К окружности с центром в точке О и радиусом 6 см проведены секущая КО и касательная KL (см. рис 38). Найдите отрезок касательной KL, если КО = 10 см. Ответ дайте в сантиметрах.
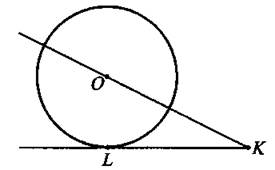
Рис. 38
Ответ: _________________.
13. Укажите в ответе номера верных утверждений.
1) Существует параллелограмм, диагонали которого взаимно перпендикулярны.
2) Если два угла одного треугольника соответственно равны двум углам другого треугольника, то такие треугольники равны.
3) Если три стороны одного треугольника соответственно равны трём сторонам другого треугольника, то такие треугольники равны.
Модуль «Реальная математика»
14. Велосипедист проехал 40 км со скоростью 25 км/ч, а затем 30 км со скоростью 20 км/ч. Сколько всего часов велосипедист был в пути?
Ответ: _________________.
15. На рисунке 39 изображён график изменения температуры воды при нагревании. По горизонтали указано время в минутах, по вертикали — значение температуры в градусах Цельсия. Сколько минут занял процесс нагревания с 10° до 80°?
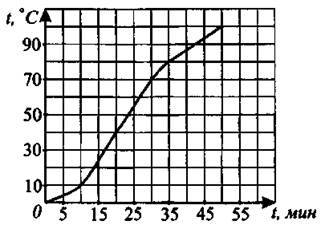
Рис. 39
Ответ: _________________.
16. Площадь загородного земельного участка горожанина составляет 10 ар и распределена между фруктовым садом и овощным огородом в отношении 4:1. Сколько ар занимает фруктовый сад?
Ответ: _________________.
17. Сколько всего осей симметрии имеет сечение гайки, изображённой на рисунке 40?
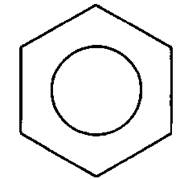
Рис. 40
Ответ: _________________.
18. На диаграмме (см. рис. 41) показана средняя температура воздуха (в °С) в городе R за каждый месяц 2010 года. Определите по диаграмме, сколько месяцев средняя температура была выше 20°С.
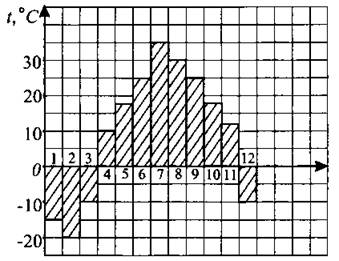
Рис. 41
Ответ: _________________.
19. На столе лежат ручки, одинаковые на вид: 8 с синей пастой и 12 с чёрной. Вася наугад берёт одну из ручек. Найдите вероятность того, что это будет ручка с синей пастой.
Ответ: _________________.
20. Вес тела (в ньютонах) при равноускоренном движении вверх вычисляется по формуле р = m(g + а), где m — масса тела (в кг), g — ускорение свободного падения (в м/с2) и а — ускорение, с которым движется лифт (в м/с2). Пользуясь формулой, найдите вес тела (в Н) массой 40 кг в лифте, движущемся вверх с ускорением 1,4 м/с2 (считайте g = 9,8 м/с2).
Ответ: _________________.
Часть 2
Задания этой части выполняйте с записью решени.
Модуль «Алгебра»
21. Решите неравенство ![]()
22. Найдите, при каких значениях га один из корней уравнения 3х2 — 15x + 2m = 0 равен 2.
23. При каких отрицательных значениях с прямая у = сх — 9 имеет с параболой у = х2 + 5х ровно одну общую точку? Найдите координаты этой точки и постройте данные графики в одной системе координат.
Модуль «Геометрия»
24. Найдите величину угла ABD, если известно, что ABCD — параллелограмм и ∠BAD = 46°, a ∠CBD = 33° (см. рис. 42).
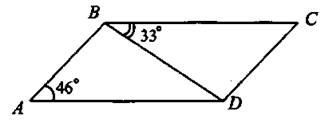
Рис. 42
25. Точки К и L лежат по одну сторону от прямой а. Перпендикуляры KF и LT, проведённые к прямой а, равны. Точка О — середина отрезка КТ. Докажите, что ∠OKL = ∠OTF.
26. Основание ВС равнобедренного треугольника АВС равно 12 см, радиус вписанной в этот треугольник окружности равен 4,5 см. Окружность радиуса R с центром O1 вне этого треугольника касается продолжений боковых сторон треугольника АВС и основания ВС в его середине. Найдите радиус R этой окружности.