Математика 9 класс подготовка к ГИА
Вариант № 3 - Учебно-тренировочные тесты
Вариант № 3
Часть 1
Модуль «Алгебра»
1. Найдите значение выражения ![]()
1) .
2) 22,.
3) -22,.
4) -27,5
2. На координатной прямой (см. рис. 15) отмечены числа а и b.
![]()
Рис. 15
Выберите наибольшее из записанных ниже чисел.
1) —b + .
2) b — .
3) а + .
4) а : b
3. Каждое из приведённых ниже выражений сложили с числом √7. Для какого выражения при этом была получена рациональная сумма?

4. Решите уравнение —х2 + 5х + 6 = 0.
Ответ: _________________.
5. Установите соответствие между графиками функций (см. рис. 16) и формулами, которые их задают.
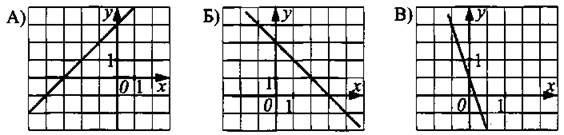
Рис. 16
1) у = х + 3
2) у = —х + 3
3) у = 3х + 1
4) у = —3х + 1
Ответ: _________________.
6. Найдите разность арифметической прогрессии, если её шестой и восьмой члены равны —4,6 и —4,2 соответственно.
Ответ: _________________.
7. Упростите выражение (b — 5) (b — 2) — b(b — 7) и найдите его значение при b = 0,27.
Ответ: _________________.
8. Решите систему неравенств ![]()
На какой из координатных прямых изображено множество её решений?

Модуль «Геометрия»
9. В ромбе MNPQ величина угла QNM равна 80° (см. рис. 17). Найдите величину угла QPM. Ответ дайте в градусах.
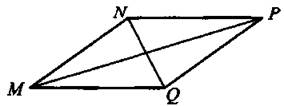
Рис. 17
10. В равностороннем треугольнике АВС радиус вписанной окружности равен 3 см (см. рис. 18). Найдите радиус описанной окружности (в см).
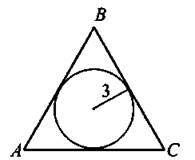
Рис. 18
Ответ: _________________.
11. Найдите площадь прямоугольника (см. рис. 19), у которого диагональ равна 5, а синус угла между диагоналями равен 0,6.
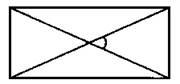
Рис. 19
Ответ: _________________.
12. Найдите длину вектора ![]()
Ответ: _________________.
13. Укажите номера верных утверждений.
1) Если в равнобедренном треугольнике угол при вершине острый, то такой треугольник — остроугольный.
2) Отношение стороны треугольника к синусу противоположного угла равно диаметру окружности, вписанной в треугольник.
3) Во всяком треугольнике высота, проведённая к основанию, совпадает с медианой.
Ответ: _________________.
Модуль «Реальная математика»
14. Настя купила бублик и разделила его между собой и тремя подружками. Сколько разломов сделала Настя?
Ответ: _________________.
15. На графике показана зависимость пройденного пешеходом расстояния от времени (см. рис. 20). По горизонтали откладывается время в минутах, по вертикали — расстояние в километрах. Сколько километров прошёл пешеход до второй остановки?
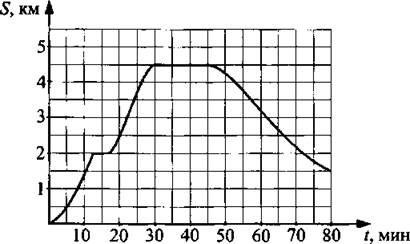
Рис. 20
Ответ: _________________.
16. Петя готовился к экзамену по геометрии. Сначала он выучил 20% всех билетов, потом четверть оставшихся. После этого ему осталось выучить 15 билетов. Сколько билетов на экзамене по геометрии?
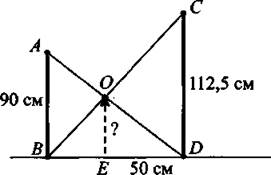
Рис. 21
Ответ: _________________.
17. Для проведения одного из этапов соревнования «Смелые и ловкие» были установлены вертикально два шеста АВ и CD разной длины на некотором расстоянии друг от друга (см. рис. 21). Концы А и D, В и С соединены верёвками, а в точке пересечения верёвок прикреплён колокольчик. Если участник проползал между верёвками так, что колокольчик не звенел, то команде присуждали одно очко. На какой высоте (в см) был подвешен колокольчик, если АВ = 90 см, CD = 112,5 см и ED = 50 см?
Ответ: _________________.
18. На диаграмме показано расстояние до звёзд Конопус, Антарес и Бетельгейзе от Земли (см. рис. 22). Известно, что Антарес в 2 раза дальше от Земли, чем Конопус, и на 100 световых лет дальше, чем Бетельгейзе. Определите, на сколько световых лет Конопус находится ближе к Земле, чем Бетельгейзе.
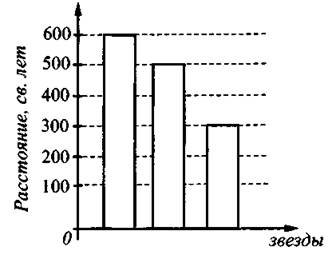
Рис. 22
Ответ: _________________.
19. Перед началом волейбольного матча капитаны команд бросают жребий, чтобы определить, какая из команд выиграет право первой подачи. Команда «Львы» по очереди играет с командами «Тигры» и «Орлы». Найдите вероятность того, что право первой подачи в обоих играх получит команда «Львы».
Ответ: _________________.
20. Вес тела при равноускоренном движении вниз вычисляется по формуле Р = m(g — а), где m — масса тела (в кг), g — ускорение свободного падения (в м/с2) и а — ускорение, с которым движется лифт (в м/с2). Пользуясь формулой, найдите вес тела (в Н) массой 70 кг в лифте, движущемся вниз с ускорением 2 м/с2 (считать д — 9,8 м/с2).
Часть 2
Задания этой части выполняйте с записью решения
Модуль «Алгебра»
21. Решите неравенство (х — 3)(х + 2) > 6.
22. От пристани А к пристани В отправился теплоход. Первые 60 км он прошёл со скоростью 30 км/ч, затем за час прошёл 25 км и оставшиеся 45 км прошёл со скоростью 22,5 км/ч. Найдите среднюю скорость теплохода. Ответ укажите в км/ч.
23. Найдите все значения а, при которых прямая, проходящая через точки (а; 0) и (0; 3), имеет с графиком функции у = 3/x только одну общую точку.
Модуль «Геометрия»
24. Гипотенуза прямоугольного треугольника равна 14. Медиана, проведённая к гипотенузе, делит прямой угол в отношении 2:1. Найдите катеты треугольника.
25. В квадрат ABCD вписан квадрат AMKN (см. рис. 23) так, что точка К делит диагональ АС в отношении 1:3, считая от точки С. Точка F — середина стороны АВ. Докажите, что ∠DKF = 90°.
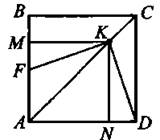
Рис. 23
26. Из точки А, лежащей на окружности, проведены две хорды АВ и АС. Точки К и F — середины хорд. Найдите радиус окружности, если АВ = 9 см, АС = 17 см, KF = 5 см.