Уроки-конспекты по Геометрии 8 класс
ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ - урок 4
Цели: рассмотреть свойство вписанного четырехугольника; учить решать задачи на применение изученного материала.
Ход урока
I. Проверка домашнего задания.
Решить устно:
1. ОK = 5, АВ = 24.
Найти: R.
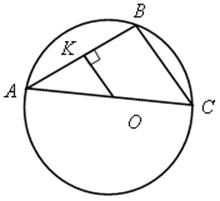
Решение
1) ![]() АОВ – равнобедренный, так как АО = ОВ = R, тогда АK = KВ.
АОВ – равнобедренный, так как АО = ОВ = R, тогда АK = KВ.
2) В ![]() АKО,
АKО, ![]() K = 90°.
K = 90°.
АО = ![]() = 13.
= 13.
2. № 705 (а).
3. Вершины треугольника АВС лежат на окружности, причем ![]() АВ :
АВ : ![]() ВС : СА = 2 : 3 : 4. Найдите углы треугольника АВС.
ВС : СА = 2 : 3 : 4. Найдите углы треугольника АВС.
4. Найти углы вписанного четырехугольника АВСD.
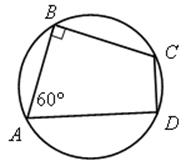
II. Изучение нового материала.
Доказательство свойства вписанного четырехугольника можно предложить учащимся разобрать самостоятельно по учебнику (хорошо успевающим – без помощи учебника).
III. Закрепление изученного материала.
Решить №№ 708 (а), 710.
IV. Самостоятельная работа.
Вариант I
Центр описанной окружности лежит на высоте равнобедренного треугольника и делит высоту на отрезки 5 см и 13 см. Найдите площадь этого треугольника.
Вариант II
Меньший из отрезков, на которые центр описанной окружности равнобедренного треугольника делит его высоту, равен 8 см, а основание треугольника равно 12 см. Найдите площадь этого треугольника.
Вариант III
(для более подготовленных учащихся)
Найдите площадь равнобедренного треугольника, в котором боковая сторона 4![]() см, а радиус описанной окружности 5 см.
см, а радиус описанной окружности 5 см.
V. Итоги урока.
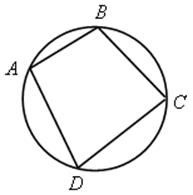
1) Если около четырехугольника описана окружность, то ![]() А +
А + ![]() С =
С = ![]() В +
В + ![]() D = 180°.
D = 180°.
2) Если ![]() А +
А + ![]() С =
С = ![]() В +
В + ![]() D = 180°, то около него можно описать окружность.
D = 180°, то около него можно описать окружность.
Домашнее задание: вопрос 1–26, с. 187–188; №№ 708 (б), 709.
Для желающих: № 729.