Уроки-конспекты по Геометрии 8 класс
ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ - урок 3
Цели: ввести понятие описанной около многоугольника окружности; рассмотреть теорему об окружности, описанной около треугольника.
Ход урока
I. Проверка домашнего задания.
Решить устно:
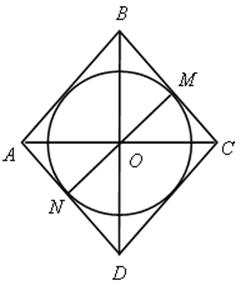
1. АВСD – ромб, СD = 32, ВС = 20.
Найти: r.
Решение
1) Из ВОС по теореме Пифагора
ОС2 = ВС2 – ОВ2 = 400 – 256 = 144
ОС = 12.
2) SАВСD = ![]() BD · AC = 32 12 = 384.
BD · AC = 32 12 = 384.
3) SАВСD = ВС · NM = 20 · MN.
384 = 20MN; MN = 19,2.
4) 2r = MN, r = 9,6.
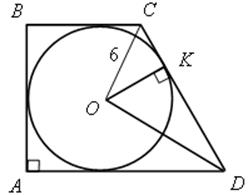
2. АВСD – трапеция,
СО = 6, ОD = 8.
Найти: SАВСD.
Решение
1) ![]() СОD – прямоугольный,
СОD – прямоугольный,
CD = ![]() = 10.
= 10.
2) SОСD = ![]() OC · OD =
OC · OD = ![]() = 24.
= 24.
3) SОСD = ![]() CD · OK =
CD · OK = 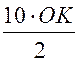 = 5 · OK.
= 5 · OK.
5ОK = 24; ОK = 4,8; ВА = 9,6.
4) АВ + СD = ВС + АD = 9,6 + 10 = 19,6.
5) SАВСD =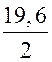 · 9,6 = 9,8 · 9,6 = 94,08 (см2).
· 9,6 = 9,8 · 9,6 = 94,08 (см2).
II. Изучение нового материала.
Изложить в виде лекции материал п. 75 до замечания 2.
III. Закрепление изученного материала.
Решить №№ 711 (для тупоугольного треугольника), 702 (а), 704 (а, б), 706.
IV. Итоги урока.
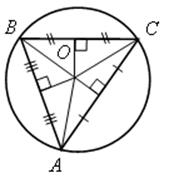
1) Центр описанной около треугольника окружности в точке пересечения серединных перпендикуляров к сторонам треугольника.
2) ОВ = ОС = ОА – радиусы описанной окружности.
3) Окружность единственная для данного треугольника.
Домашнее задание: вопросы 24, 25, с. 188; №№ 711 (для прямоугольного и равностороннего треугольников), 702 (б), 705 (б).