Уроки-конспекты по Геометрии 8 класс
ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ - урок 2
Цели: доказать свойство описанного четырехугольника и научить применять его при решении задач.
Ход урока
I. Проверка домашнего задания.
1. № 690 и № 693 (а) вынести решение на доску.
2. Решить устно.
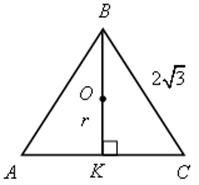
1) Найдите радиус окружности, вписанной в равносторонний треугольник, если сторона треугольника 2![]() .
.
2) Найдите радиус окружности, вписанной в треугольник со сторонами 10 см, 10 см, 12 см.
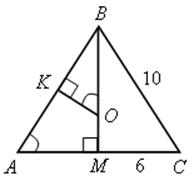
Решение
ВМ = ![]() = 8
= 8
ОМ = r, ВО = 8 – r
![]() АВМ
АВМ ![]() ОВK (угол В – общий).
ОВK (угол В – общий).
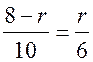 ; r = 3.
; r = 3.
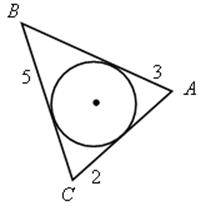
3) Найти периметр треугольника АВС.
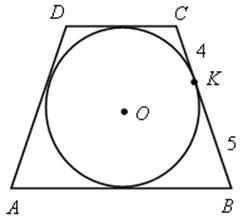
4) АВСD – равнобедренная трапеция.
Найти: DС и АВ.
II. Изучение нового материала.
1. Рассмотреть свойство описанного четырехугольника.
2. Решение задачи № 697.
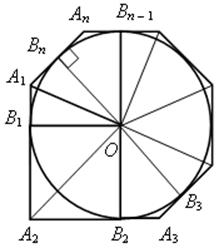
Пусть окружность радиуса r с центром О вписана в многоугольник А1А2 … Аn и пусть В1, В2, .., Вn – точки касания.
Тогда ОВ1 = ОВ2 = … = ОВn = r и ОВ1 ![]() А1А2, ОВ2
А1А2, ОВ2 ![]() А2А3, .., ОВn
А2А3, .., ОВn ![]() А1Аn.
А1Аn.
![]()
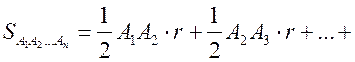
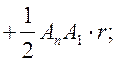
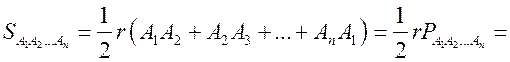 рr, где р – полупериметр многоугольника.
рr, где р – полупериметр многоугольника.
S = pr
III. Закрепление изученного материала.
Выполнить № 695 (устно), № 698.
IV. Самостоятельная работа обучающего характера.
Вариант I
Гипотенуза прямоугольного треугольника равна 10 см, радиус вписанной в этот треугольник окружности 2 см. Найдите периметр треугольника и его площадь.
Вариант II
Радиус окружности, вписанной в прямоугольный треугольник, равен 2 см, а сумма катетов равна 17 см. Найдите периметр треугольника и его площадь.
Вариант III
(для более подготовленных учащихся)
Докажите, что радиус окружности, вписанной в равнобедренную трапецию с основаниями а и b, равен 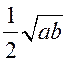 .
.
Решение можно проверить в классе с помощью закрытой доски.
Вариант I
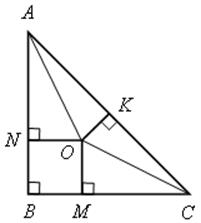
Используя решение задачи № 693, имеем РАВС = 2 (АС + r) = 2(10 + 2) = 24 (см).
SАВС = р · r = 12 · 2 = 24 (cм2).
Вариант II
Используя решение задачи № 693, имеем
АВ + ВС = AN + NB + MB + CM = АK + r + r + KС
АВ + ВС = АС + 2r; АС = АВ + ВС – 2r
РАВС = 2 (АС + r) = 2 (АВ + ВС – 2r + r)
РАВС = 2(17–2) = 30 (cм)
SАВС = р · r = 15 · 2 = 30 (cм2).
Вариант III
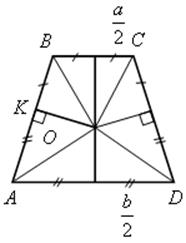
1) ![]() АВС +
АВС + ![]() ВАД = 180°.
ВАД = 180°.
ВО и АО – биссектрисы.
![]() ОАВ +
ОАВ + ![]() ОВА = 90°, тогда
ОВА = 90°, тогда ![]() АОВ = 90°.
АОВ = 90°.
2) ОК = 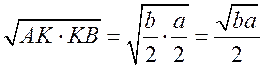 .
.
V. Итоги урока.
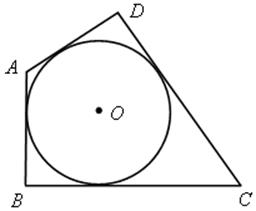
1. АВСD – четырехугольник;
1) АВ + DС = АD + ВС, можно вписать окружность;
2) если вписана окружность, то АВ + DС = АD + ВС.
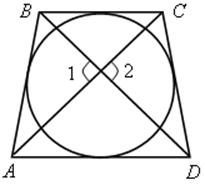
2. АВСD – равнобокая трапеция
1) АВ + DС = ВС + АD, если вписана окружность и наоборот.
2) ![]() 1 =
1 = ![]() 2 = 90°.
2 = 90°.
3) r = 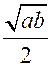 .
.
Для разносторонней трапеции выполняются только 1-е и 2-е свойства.
Домашнее задание: вопрос 23, с. 188; № 641, № 696, повторить решение задачи № 697.
Для желающих.
АВСD – трапеция, описанная вокруг окружности. АВ = СD, ВD = 5, SАВСD = 12.
Найти: РАВСD.
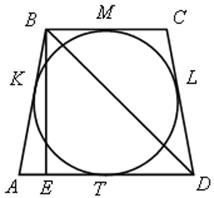
Решение
1) ВK = ВМ = ЕТ
KА = LD = DТ
2) Тогда ВK = ЕТ, KА = DТ.
3) Поэтому ЕD = АВ.
4) Пусть АВ = ЕD = х.
5) ВЕ = ![]() .
.
6) SАВСD = 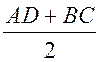 ∙ BE =
∙ BE = 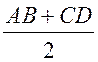 ∙ BE = AB ∙ BE
∙ BE = AB ∙ BE
SАВСD = x![]()
122 = х2 (25 – х2)
144 = 25х2 – х4
х1 = 4, х2 = 3; АВ = 4, АВ = 3 не удовлетворяет условию задачи.
РАВСD = 4 АВ = 16.