Уроки-конспекты по Геометрии 8 класс
ПРИМЕНЕНИЕ ПОДОБИЯ К ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ И РЕШЕНИЮ ЗАДАЧ - урок 5
Цели: проверить степень усвоения учащимися изученного материала и умения применять его к решению задач; рассмотреть решение задач на построение методом подобия.
Ход урока
I. Проверка домашнего задания.
II. Проверочная самостоятельная работа.
Скомпоновать для каждого ученика вариант из таблицы.
Таблица
Элементы |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
a |
6 |
5 |
1 |
12 |
||||||||
b |
8 |
24 |
40 |
5 |
||||||||
c |
13 |
25 |
100 |
29 |
10 |
|||||||
hc |
|
144 |
8 |
4,8 |
||||||||
ac |
36 |
3 |
108 |
7,2 |
5 |
|||||||
bc |
15 |
13 |
Ответы:
1) 10; 4,8; 3,6; 6,4.
2) 12; 4![]() ; 1
; 1![]() ; 11
; 11![]() .
.
3) 7; 6,72; 1,96; 23,04.
4) 60; 80; 48; 64.
5) 20; 21; 14![]() ; 13
; 13![]() .
.
6) ![]()
7) 3; 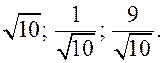
8) 180; 240; 300; 192.
9) 9; 41; 1![]() ; 39
; 39![]() .
.
10) 16; 20; 9,6; 12,8.
11) ![]()
12) 8; 6; 6,4; 3,6.
Можно организовать тесты с выбором ответа. Второе или третье задание самостоятельной работы может быть таким: начертите отрезок и разделите его в отношении а : b.
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
а |
2 |
4 |
3 |
5 |
2 |
3 |
5 |
4 |
2 |
3 |
6 |
5 |
b |
7 |
5 |
8 |
3 |
6 |
7 |
6 |
3 |
5 |
6 |
4 |
2 |
III. Объяснение нового материала.
1. Вспомнить с учащимися задачи на построение.
Начертите остроугольный треугольник АВС. Постройте а) медиану АМ, биссектрису АD и высоту АН треугольника АВС; б) прямую BN, параллельную медиане АМ. (Нет необходимости требовать, чтобы учащиеся фактически выполнили все построения циркулем и линейкой, достаточно, если они укажут в каждом случае последовательность выполнения операций.)
2. Задача 3 из п. 64.
IV. Решение задач.
№ 589.
Решение
![]()
Дано: Анализ (устно). Пусть ![]() АВС – искомый. Тогда любой треугольник А1В1С1, в котором А1В1 || АВ (А1
АВС – искомый. Тогда любой треугольник А1В1С1, в котором А1В1 || АВ (А1 ![]() АС, В1
АС, В1 ![]() ВС), подобен треугольнику АВС по первому признаку подобия (
ВС), подобен треугольнику АВС по первому признаку подобия (![]() А1=
А1= ![]() А,
А, ![]() С – общий). Следовательно, А1В1 : А1С = 2 : 1.
С – общий). Следовательно, А1В1 : А1С = 2 : 1. ![]() А1 =
А1 = ![]() hk. Таким образом, достаточно построить какой-нибудь треугольник А1В1С, в котором А1В1 : А1С = 2 : 1,
hk. Таким образом, достаточно построить какой-нибудь треугольник А1В1С, в котором А1В1 : А1С = 2 : 1, ![]() А1 =
А1 = ![]() hk, а затем отложить на луче СВ1 отрезок СВ = PQ и через точку В провести прямую, параллельную прямой А1В1. Точка А пересечения этой прямой с прямой А1С является вершиной искомого треугольника.
hk, а затем отложить на луче СВ1 отрезок СВ = PQ и через точку В провести прямую, параллельную прямой А1В1. Точка А пересечения этой прямой с прямой А1С является вершиной искомого треугольника.
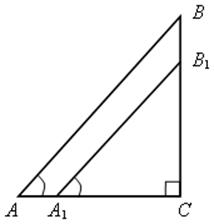
Построение.
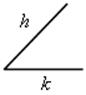
1. Строим угол МА1N, равный данному углу hk.
2. Отмечаем произвольную точку С на луче А1N.
3. На луче А1М откладываем отрезок А1В1, равный 2А1С.
4. На луче СВ1 откладываем отрезок СВ, равный данному отрезку РQ.
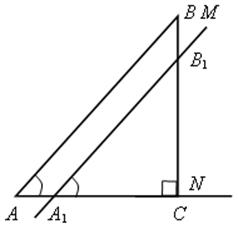
5. Через точку В проведем прямую, параллельную А1В1. Она пересекает прямую А1С в точке А. Треугольник АВС – искомый.
Доказательство. ![]() АВС
АВС ![]()
![]() А1В1С1 по двум углам (
А1В1С1 по двум углам (![]() А =
А = ![]() А1 =
А1 = ![]() hk, так как АВ || А1В1,
hk, так как АВ || А1В1, ![]() С – общий), поэтому АВ : АС = А1В1 : А1С = 2 : 1. Треугольник АВС – искомый, так как
С – общий), поэтому АВ : АС = А1В1 : А1С = 2 : 1. Треугольник АВС – искомый, так как ![]() А =
А = ![]() hk, ВС = РQ по построению АВ : АС = 2 : 1.
hk, ВС = РQ по построению АВ : АС = 2 : 1.
Исследование (устно). Указанный способ решения задачи показывает, что задача всегда имеет решение. Все треугольники, удовлетворяющие условиям задачи, подобны по второму признаку подобия треугольников. (![]() А =
А = ![]() hk, АВ : АС = 2 : 1), следовательно, их углы соответственно равны, а так как в любом из этих треугольников ВС = РQ, то все они равны по второму признаку равенства треугольников. Таким образом, задача имеет единственное решение.
hk, АВ : АС = 2 : 1), следовательно, их углы соответственно равны, а так как в любом из этих треугольников ВС = РQ, то все они равны по второму признаку равенства треугольников. Таким образом, задача имеет единственное решение.
V. Итоги урока.
Домашнее задание: вопрос 12, с. 161; №№ 586, 587 (обязательно прокомментировать).
№ 586.
Дано: ![]() А,
А, ![]() В,
В, ![]() В >
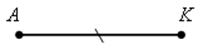
В > ![]() А, АK – биссектриса
А, АK – биссектриса ![]() А.
А.
Построить ![]() АВС.
АВС.
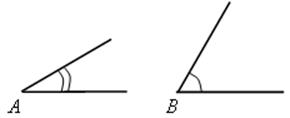
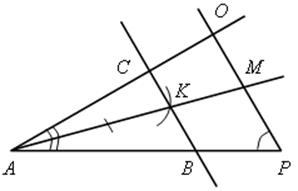
Построение.
1) От произвольного отрезка АР отложим углы ![]() А и
А и ![]() Р =
Р = ![]() В.
В.
2) Точка О пересечения сторон углов А и Р.
3) Разделим ![]() А пополам биссектрисой АМ.
А пополам биссектрисой АМ.
4) На луче АМ отложим отрезок АK.
5) Проведем через точку K прямую СВ || ОР.
6) Полученный треугольник АВС – искомый.
№ 587.
Решение
Дано: ![]() А,
А, ![]() В, Н – высота, проведенная из вершины
В, Н – высота, проведенная из вершины ![]() С.
С.
Построить ![]() АВС.
АВС.
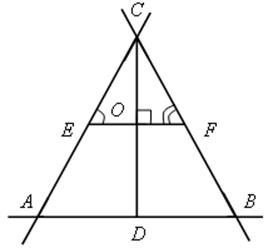
![]()
Построение.
1) От произвольного отрезка ЕF отложим углы![]() Е =
Е = ![]() А,
А, ![]() F =
F =![]() B.
B.
2) C – точка пересечения сторон ![]() Е и
Е и ![]() F, отличных от EF.
F, отличных от EF.
3) Из точки С опустим перпендикуляр к отрезку EF.
4) О – точка пересечения перпендикуляра и отрезка ЕF.
5) От точки С на луче СО отложим высоту СD = Н.
6) Проведем через точку D прямую АВ || EF до пересечения с продолжением отрезков СЕ и СF.
7) Полученный треугольник АВС – искомый.