Уроки-конспекты по Геометрии 8 класс
ПРИМЕНЕНИЕ ПОДОБИЯ К ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ И РЕШЕНИЮ ЗАДАЧ - урок 6
Цель: закрепить умение решения задач на построение методом подобия.
Ход урока
I. Проверка домашнего задания.
Рассмотреть решение задач № 586, № 587.
II. Анализ самостоятельной работы.
III. Решение задач.
№ 590.
Решение
Дано:
![]()
![]()
![]()
Построить: ![]() АВС,
АВС, ![]() С = 90°, АВ = PQ,
С = 90°, АВ = PQ, 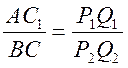 .
.
Анализ. Задачу будем решать методом подобия. Сначала можно построить какой-нибудь прямоугольный треугольник АВ1С1 (![]() С1 = 90°) так, чтобы
С1 = 90°) так, чтобы 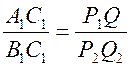 , а затем, используя условие АВ = PQ, построить искомый треугольник АВС.
, а затем, используя условие АВ = PQ, построить искомый треугольник АВС.
Построение.
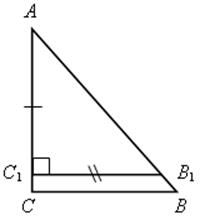
1. Строим треугольник АВ1С1 так, чтобы ![]() С1 = 90°, С1А = Р1Q, С1В1 = Р2Q2 (п. 38, зад. 1).
С1 = 90°, С1А = Р1Q, С1В1 = Р2Q2 (п. 38, зад. 1).
2. На луче АВ1 отложим отрезок АВ = РQ.
3. Через точку В проведем прямую, параллельную В1С1. Она пересекает луч АС1 в точке С. Треугольник АВС – искомый.
Доказательство.
![]() АВС
АВС ![]()
![]() А1В1С1 по первому признаку подобия треугольников (
А1В1С1 по первому признаку подобия треугольников (![]() А – общий,
А – общий, ![]() С =
С = ![]() С1, так как ВС || В1С1), поэтому
С1, так как ВС || В1С1), поэтому ![]() С = 90°,
С = 90°, 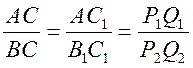 .
.
Сторона АВ равна данному отрезку PQ по построению. Итак, треугольник АВС удовлетворяет всем условиям задачи.
Исследование.
Из построения следует, что задача при любых данных отрезках PQ, Р1Q1 и P2Q2 имеет решение. Задача имеет единственное решение. В самом деле, если ![]() А1В1С1 и
А1В1С1 и ![]() А2В2С2 удовлетворяют условиям задачи, то они подобны, а так как А1В1 = РQ, А2В2 = РQ, то А1В1 = А2В2 и, значит,
А2В2С2 удовлетворяют условиям задачи, то они подобны, а так как А1В1 = РQ, А2В2 = РQ, то А1В1 = А2В2 и, значит, ![]() А1В1С1 =
А1В1С1 = ![]() А2В2С2.
А2В2С2.
№ 622.
Дано: ![]() АВС.
АВС.
Построить ![]() А1В1С1 :
А1В1С1 : ![]() = 2SАВС и
= 2SАВС и ![]() А1В1С1
А1В1С1 ![]()
![]() АВС.
АВС.
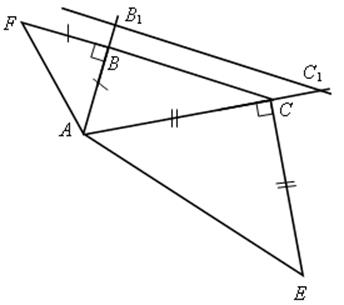
Построение.
1) Построим ![]() АВF так, чтобы АВ
АВF так, чтобы АВ ![]() ВF и BF = АВ (как описано в задаче № 290).
ВF и BF = АВ (как описано в задаче № 290).
2) Построим ![]() АCЕ так, чтобы СЕ
АCЕ так, чтобы СЕ![]() АС и СЕ = АС аналогично.
АС и СЕ = АС аналогично.
3) На лучах АВ и АС отложим соответственно отрезки АВ1 = AF и АС1 = АЕ.
4) Проведем отрезок В1С1.
5) Тогда ![]() АВ1С1 – искомый.
АВ1С1 – искомый.
Доказательство.
1) По теореме Пифагора
![]()
![]()
2) По построению AB1 = AF = ![]() AB.
AB.
AC1 = AE = ![]() AC.
AC.
3) 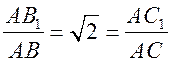 .
.
4) ![]() А1В1С1
А1В1С1 ![]()
![]() АВС (по второму признаку).
АВС (по второму признаку).
5) 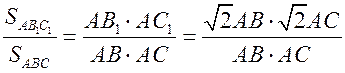 = 2.
= 2.
Поэтому ![]() АВ1С1 удовлетворяет всем условиям задачи.
АВ1С1 удовлетворяет всем условиям задачи.
IV. Самостоятельная работа.
Вариант I
Постройте прямоугольный треугольник по острому углу и медиане, проведенной из вершины этого угла.
Вариант II
Постройте прямоугольный треугольник по острому углу и биссектрисе прямого угла.
Вариант III
(для наиболее подготовленных учащихся)
Постройте ромб по стороне и данному отношению 3 : 4 его диагоналей.
V. Итоги урока.
Домашнее задание: вопросы 8–12 на с. 160–161; № 588, прочитать п. 65.
№ 588.
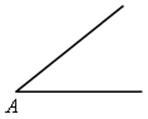
Дано: ![]() А,
А, 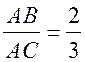 , AM – медиана.
, AM – медиана.
![]()
![]()
![]()
![]()
Построить: ΔАВС.
Построение.
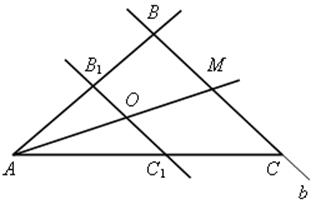
1) На произвольной прямой отметим произвольно точку А и отложим ![]() А.
А.
2) Пусть а – произвольный единичный отрезок.
3) На сторонах ![]() А отложим отрезки АВ1 = 2а и АС1 = 3а.
А отложим отрезки АВ1 = 2а и АС1 = 3а.
4) Проведем В1С1 и разделим его пополам точкой О.
5) Проведем луч АО и отложим отрезок АМ.
6) Через точку М проведем прямую b || B1C1; точки пересечения со сторонами угла А обозначим В и С.
7) ![]() АВС – искомый.
АВС – искомый.
Доказательство.
1) ![]() АВС
АВС ![]()
![]() АВ1С1 (
АВ1С1 (![]() A – общий,
A – общий, ![]() AВ1С1 =
AВ1С1 = ![]() AВС, как соответственные при ВС || B1C1 и секущей АВ).
AВС, как соответственные при ВС || B1C1 и секущей АВ).
2) 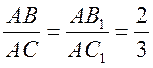 .
.
3) Аналогично доказывается, что 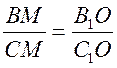 = 1.
= 1.
4) Полученный ![]() АВС – искомый, так как АМ – медиана,
АВС – искомый, так как АМ – медиана, 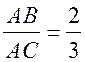 по доказанному.
по доказанному.