Уроки-конспекты по Геометрии 8 класс
ПРИМЕНЕНИЕ ПОДОБИЯ К ДОКАЗАТЕЛЬСТВУ ТЕОРЕМ И РЕШЕНИЮ ЗАДАЧ
Цели: ввести определение средней линии треугольника, сформулировать и доказать теорему о средней линии треугольника; рассмотреть решение задач на применение этой теоремы и задачу о свойстве медиан треугольника.
Ход урока
I. Анализ контрольной работы.
II. Решение задач.
Решите устно:
1. АО : ОС = ВО : ОD. Докажите, что АВСD – трапеция или параллелограмм.
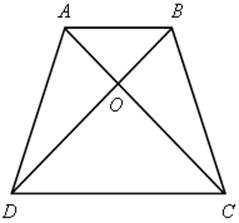
Решение
По второму признаку подобия треугольников ![]() АВО
АВО ![]()
![]() CОD, поэтому
CОD, поэтому ![]() BАО =
BАО = ![]() ОСD, тогда АВ || DС.
ОСD, тогда АВ || DС.
АВСD – трапеция.
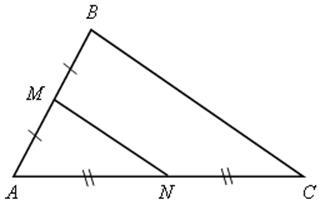
2. М и N – середины сторон АВ и ВС. Докажите, что MN || АС.
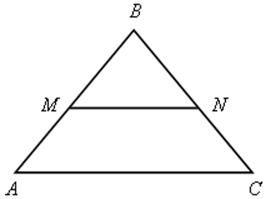
Решение
По второму признаку подобия треугольников![]() АВС
АВС ![]()
![]() МВN, поэтому
МВN, поэтому ![]() BMN =
BMN = ![]() АВС, тогда MN || AС.
АВС, тогда MN || AС.
III. Объяснение нового материала.
1. Дать определение средней линии треугольника.
2. Сформулировать теорему о средней линии треугольника.
3. Доказательство теоремы можно предложить учащимся провести самостоятельно.
IV. Закрепление изученного материала.
1. № 564 (устно).
2. № 567.
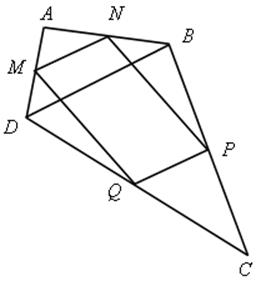
Решение
1) MN – средняя линия ![]() АВD.
АВD.
MN || DВ и MN = ![]() DВ.
DВ.
2) РQ – средняя линия ![]() СВD.
СВD.
PQ || DВ и PQ = ![]() DВ.
DВ.
3) Имеем MN || DВ и PQ || DВ, поэтому MN || PQ.
4) Получили MN PQ и MN = PQ = ![]() DВ, следовательно, четырехугольник MNPQ – параллелограмм.
DВ, следовательно, четырехугольник MNPQ – параллелограмм.
3. Задача 1 из § 3, с. 146–147 учебного пособия.
4. № 570.
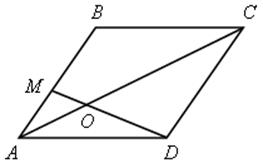
Решение
1) ![]() АМО
АМО ![]()
![]() СDО (по двум углам
СDО (по двум углам ![]() MАО =
MАО = ![]() DСО и
DСО и ![]() АОМ =
АОМ = ![]() СОD).
СОD).
2) 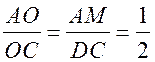 .
.
V. Итоги урока.
Если АМ = МВ и МN = NC, то MN || ВC, MN = ![]() BC.
BC.
АА1, СС1, ВВ1 – медианы треугольника АВС.
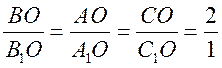 (считать от вершины).
(считать от вершины).
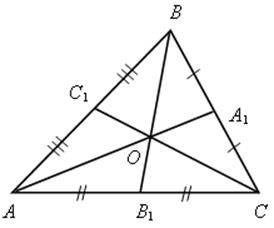
Домашнее задание: вопросы 8, 9, с. 160; №№ 565, 566, 571.
№ 571.
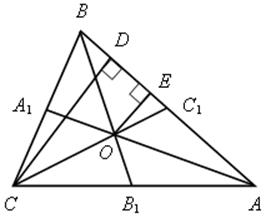
Решение
1) Пусть СС1 – медиана треуголь-ника АВС, СD и ОЕ – высоты треугольников АВС и АОВ.
2) Так как 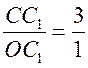 , то
, то 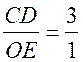 , то есть СD = 3 · ОЕ.
, то есть СD = 3 · ОЕ.
3) SАВС = 3SАОВ = 3S.