Корень n-й степени - Степенная функция. Корень n-й степени - Квадратичная функция

Цель: рассмотреть понятие корня натуральной степени п.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Дана функция f(x) = 2(х - 1)4. Вычислите 2f(0) – 3f(1) + 4f(2).

2. Сравните числа.

а) (-7,2)6 и (6,1)6;

б) (-4,8)3 и 2,73.

3. Постройте график функции у = (х + 1)4 - 2.

Вариант 2

1. Дана функция f(x) = -2(х + 1)3. Вычислите 6f(-1) + 4f(0) – 3f(1).

2. Сравните числа.

а) (-9,3)4 и (7,3)4;

б) (-7,8)5 и 4,75.

3. Постройте график функции у = (х + 1)3 - 2.

III. Изучение нового материала

Вы уже знаете, что понятие квадратного корня возникло при решении простейшего квадратного уравнения х2 = а. При этом квадратным корнем из числа а называют такое число, квадрат которого равен а. Разумеется, кроме уравнения х2 = а необходимо решать уравнения х3 = а, х4 = а, ..., хn = а. Поэтому надо ввести понятие корня любой натуральной степени n (аналогичное понятию квадратного корня).

Корнем n-й степени из числа а называют такое число, n-я степень которого равна а. Этот корень обозначают символом Причем n называют показателем корня, а - подкоренным выражением.

Пример 1

т. к. 05 = 0.

Принято корень второй степени называть квадратным корнем, корень третьей степени - кубическим корнем.

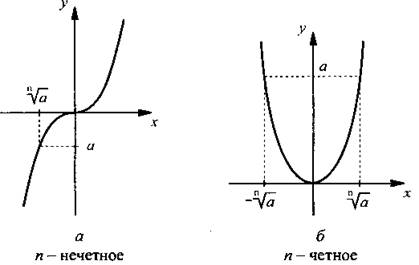
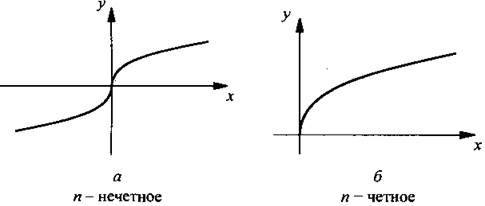
Теперь необходимо уточнить понятие корня. Сначала рассмотрим степенную функцию у = хn с нечетным показателем n. Из рис. а видно, что для любого значения а уравнение хn = а имеет единственное решение Обратимся теперь к степенной функции у = хn с четным показателем n (рис. б).

Тогда уравнение хn = а при а < 0 решений не имеет, при а = 0 имеет единственное решение х = 0, при а > 0 имеет два противоположных по знаку решения. В этом случае положительное решение обозначают символом

Пример 2

Рассмотрим уравнение х4 = 81. Очевидно, что такое уравнение имеет два решения: x1 = -3 и х2 = 3, т. к. при подстановке этих чисел в уравнение получаем верное равенство. Учитывая, что такие решения можно записать в виде и

Таким образом, выражение при а ≥ 0 имеет смысл при четном и нечетном и, и значение этого выражения является неотрицательным числом. Его называют арифметическим корнем n-й степени из а. Арифметическим корнем n-й степени из неотрицательного числа а называют такое неотрицательное число, n-я степень которого равна а.

Корень нечетной степени из отрицательного числа можно выразить через арифметический корень из положительного числа.

Пример 3

Получаем

Ранее изученные свойства квадратного корня можно обобщить на случай корня n-й степени:

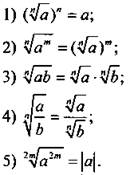
В равенствах 1-5 числа m и n - натуральные, в равенствах 1-4 числа а, b ≥ 0 и в равенстве 4 число b ≠ 0.

Пример 4

Используя приведенные свойства, вычислим.

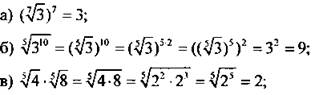
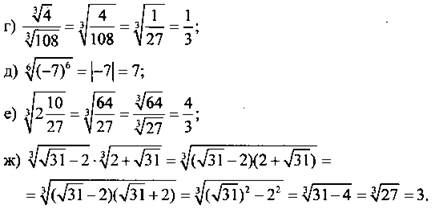
В заключение приведем графики функций для нечетных (рис. а) и четных (рис. б) значений n.

IV. Контрольные вопросы

1. Определение корня n-й степени.

2. Основные свойства корня n-й степени.

3. Графики функции для нечетных и четных значений n.

V. Задание на уроке

№ 159 (а, г, ж); 160 (д); 162; 164; 168 (д); 171 (в); 173; 177 (а); 178 (б); 179.

VI. Задание на дом

№ 159 (б, в, з); 160 (е); 163; 165; 168 (е); 171 (г); 174; 177 (в); 178(a).

VII. Подведение итогов урока