Деление многочленов - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цель: изучить деление многочлена на многочлен.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Найти допустимые значения переменной и упростить дробь

2. Известно, что Найти

3. При каких целых значениях n выражение также является целым числом? Какое это число?

Вариант 2

1. Найти допустимые значения переменной и упростить дробь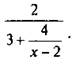

2. Известно, что Найти

3. При каких целых значениях n выражение также является целым числом? Какое это число?

III. Изучение нового материала (основные понятия)

С необходимостью деления двух многочленов (одной переменной) мы встретились на предыдущем занятии. Рассмотрим этот вопрос более подробно. При делении многочлена степени n на многочлен степени m (n ≥ m) в частном получается многочлен степени n — m и в остатке — многочлен степени m — 1. Процесс деления многочленов аналогичен процессу деления натуральных чисел «уголком» и осуществляется таким образом, чтобы на каждом промежуточном этапе деления исчезала старшая степень делимого многочлена.

Пример 1

Разделим многочлен четвертой степени А = х4 - 2х3 - 2х + 3 на многочлен второй степени В = х2 - 3х +1.

Выполним такое деление уголком. Первое слагаемое частного

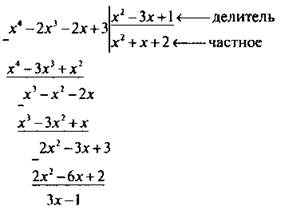
получается делением старшего члена делимого на старший член делителя (х4 : х2 = х2). Затем это слагаемое (х2) умножается на делитель х2 - 3х + 1. Получаем x2(x2 -3 x + 1) = x4 + 3x3 + x2. Этот результат вычитается из делимого и получается первый остаток х3 - х2. К этому остатку сносим следующий член делимого -2х. Имеем многочлен х3 - х2 - 2х.

Этот многочлен x3 - х2 - 2х воспринимается как новое делимое и повторяется тот же процесс. Старший член многочлена х3 делится на старший член делителя (х3 : х2 = х). Получаем второе слагаемое частного (х). Это слагаемое х умножается на делитель х2 - 3х + 1. Имеем х4 - 3х3 + х2. Этот результат вычитается из делимого и получается второй остаток 2х2 - 3х. К этому остатку сносим следующий последний член делимого 3. Имеем многочлен 2x2 - 3х + 3.

Полученный многочлен 2х2 - 3х + 3 считаем новым делимым и вновь повторяем процесс. Старший член многочлена делим на старший член делителя (2х2 : х2 = 2). Имеем третье слагаемое частного (2). Это слагаемое 2 умножается на делитель х2 - 3х + 1. Получаем 2(х2 - 3х + 1) = 2х2 - 6х + 2. Этот результат вычитаем из делимого и получаем многочлен первой степени 3х + 1. Так как степень этого остатка (первая) меньше степени делителя (вторая), то на этом процесс деления заканчивается.

Итак, при делении многочлена А на многочлен В в частном получаем многочлен второй степени х2+х + 2, в остатке — многочлен первой степени Зх + I. Как и в случае деления чисел, делимое можно представить в виде: делимое = делитель • частное + остаток.

В данном случае можно записать: х4 - 2х3 - 2х + 3 = (х2 - 3х + 1)(х2 + х + 2) + (3х + 1). В справедливости этого равенства легко убедиться, если в правой части раскрыть скобки и привести подобные члены.

Может оказаться, что при делении одного многочлена на другой остаток равняется нулю, т. е. один многочлен без остатка делится на другой.

Пример 2

Разделим многочлен четвертой степени А = 2х4 + 3х3 + 2х2 + 14х + 3 на многочлен второй степени В = х2 - х + 3.

Разделим данные многочлены уголком и получим.

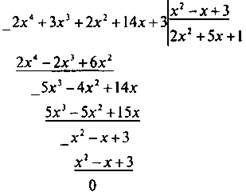
Видно, что в частном получается многочлен второй степени 2х2 + 5х + 1, в остатке — ноль. Поэтому можно записать: 2х4 + 3x3 + 2х2 + 14x + 3 = (х2 – х + 3)(2х2 + 5х + 1), т. е. делимое = делитель • частное.

Пример 3

При каких целых значениях а рациональная дробь также будет целым числом? Найдите эти числа.

В дроби А выделим целую часть. Для этого разделим ее числитель на знаменатель. При делении получили в частном

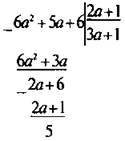
3а + 1, в остатке — число 5. Поэтому числитель дроби можно записать в виде 6a2 + 5a + 6 = (2a + 1)(3a + 1) + 5. Используя свойство сложения, выделим в дроби А целую часть. Получаем:

Так как по условию число а целое, то значение выражения 3а + 1 также будет целым числом. Поэтому требуется, чтобы дробь была целым числом. Это возможно только в том случае, если ее знаменатель является делителем числителя. Числитель дроби имеет четыре делителя: ±1 и ±5. Рассмотрим эти случаи.

а) 2а + 1 = 1. Из этого уравнения а = 0 и дробь A = 1 + 5 = 6.

б) 2a + 1 = -1. Корень этого уравнения а = -1 и дробь

в) 2а + 1 = 5. Из уравнения находим а = 2 и дробь

г) 2а + 1 = -5. Корень этого уравнения а = -3 и дробь

Итак, при а = 0 А = 6, при а = -1 А = -7, при а = 2 А = 8, при а = -3 А = -9.

Пример 4

Найти целочисленные решения уравнения 2ху + y + 6x - 9 = 0 (т. е. те решения, которые являются целыми числами).

Сначала изданного уравнения выразим одну из переменных, например y. Получаем: 2ху + у = -6х + 9 или (2х + 1)у = -6х + 9. Так как по условию х — целое число, то выражение 2х + 1 ≠ 0. Разделим обе части уравнения на 2х + 1 и получим По условию величина у должна быть целым числом. Так как число -3 целое, то дробь также должна быть целым числом. Это возможно, если знаменатель дроби является делителем числителя. Числитель 12 имеет делители: ±1; ±2; ±3; ±4; ±6; ±12. При целых значениях х величина 2х + 1 будет нечетным числом. Поэтому надо рассмотреть четыре случая.

а) 2a + 1 = 1. Из этого уравнения найдем х = 0 и тогда

б) 2а + 1 = -1. Корень этого уравнения х = -1, тогда

в) 2а + 1 = 3. Из этого уравнения находим х = 1 и тогда

г) 2а + 1 = -3. Корень этого уравнения х = -2, тогда

Итак, данное уравнение имеет четыре целочисленных решения: (0; 9), (-1; —15), (1; 1), (-2;-7).

IV. Задание на уроке и дома

1. Разделите многочлен А на многочлен В:

Ответы: а) частное 3х + 2, остаток 0;

б) частное 2х - 1, остаток 0;

в) частное 0, остаток 3х + 4;

г) частное 0, остаток 5х - 4;

д) частное 2x2 - 5х + 1, остаток 2;

е) частное 3х2 - х + 5, остаток -4;

ж) частное 2х2 - 3х + 1, остаток 3х - 5;

з) частное 3х2 - х + 1, остаток -3х + 5.

2. При каких целых значениях а дробь А также будет целым числом? Найти это число.

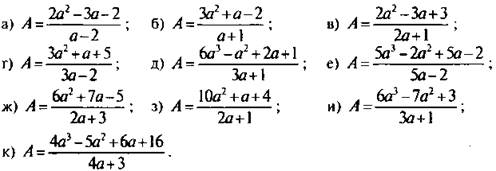
Ответы: а) при любых а, кроме a = 2, A = 2a + 1;

б) при любых а, кроме a = -1, А = 3а - 2;

в) а = 0 А = 3, а = -1 А = -8, а = 2 А = 1, a = -3 А = -6;

г) a = 1 A = 9, а = 3 A = 5;

д) при любых а А = 2a2 - a + 1;

е) при любых a А = a2 + 1;

ж) таких а нет;

з) таких а нет;

и) а = 0 А = 3, а = -1 А = 5.

к) а = -1 А = -1 ,а = 1 А = 3.

3. Найти целочисленные решения уравнения:

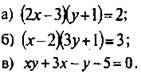
Ответы: а) (2; 1), (1; -3); б) (5; 0); в) (2; -1), (0; -5), (3; -2), (-1; -4).

V. Подведение итогов урока