Преобразование рациональных выражений - ПРОИЗВЕДЕНИЕ И ЧАСТНОЕ ДРОБЕЙ - РАЦИОНАЛЬНЫЕ ДРОБИ

Цель: освоить навыки преобразования рациональных выражений.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Разделите многочлен 3х3 + 5х2 - 7х +2 на двучлен х + 1. Укажите частное и остаток.

2. Найдите целочисленные решения уравнения (2x – 1)(x + у) = 3.

Вариант 2

1. Разделите многочлен 4x3 - 7х2 + 6х + 3 на двучлен х - 1. Укажите частное и остаток.

2. Найдите целочисленные решения уравнения (3x – 1)(2x + у) = 5.

III. Изучение нового материала (основные понятия)

Пример 1

Рассмотрим рациональное выражение

Оно представляет собой произведение двух множителей. Первый множитель является суммой двух рациональных дробей Результатом сложения будет также рациональная дробь.

Второй множитель является разностью одночлена х и рациональной дроби Одночлен х можно представить в виде дроби со знаменателем 1. Тогда разностью двух рациональных дробей также будет рациональная дробь.

Последней операцией является умножение двух рациональных дробей. Произведением их вновь будет рациональная дробь.

Из примера видно, что преобразование любого рационального выражения сводится к сложению, вычитанию, умножению и делению рациональных дробей (как следует из правил действий с дробями). Поэтому любое рациональное выражение можно представить в виде рациональной дроби.

Пример 2

Преобразуем выражение из примера 1 в рациональную дробь.

Выражение можно преобразовать по действиям, при достаточной практике преобразования можно выполнять и сразу. Рассмотрим эти подходы.

Способ 1. Сначала выполним сложение дробей в первой скобке. Эта операция будет первым действием:

Теперь во второй скобке из одночлена вычтем дробь. Такая операция будет вторым действием:

Наконец, умножим рациональные дроби, полученные в первом и втором действиях. Эта операция будет третьим действием:

В результате преобразований была получена рациональная дробь. В данном случае такая дробь представляет собой число 1.

Способ 2. Параллельно будем выполнять сложение в первой скобке и вычитание во второй скобке. Тогда получим:

В ряде задач встречаются выражения, которые необходимо упростить (сокращением дроби) до начала выполнения операций.

Пример 3

Упростим выражение

Обратим внимание на то, что числитель первой дроби является квадратом суммы, а числитель второй дроби — квадратом разности (формулы сокращенного умножения). Поэтому имеем:

При преобразованиях громоздких дробей (числители и знаменатели которых в свою очередь представляют собой дроби) полезно использовать основное свойство дроби.

Пример 4

Упростим выражение

Преобразования данного выражения можно выполнить по-разному. Можно преобразовать числитель и знаменатель дроби, затем разделить первый результат на второй. Проще использовать основное свойство дроби. Общий знаменатель в числителе и знаменателе равен ab. Поэтому умножим числитель и знаменатель данной дроби на выражение ab. Получаем:

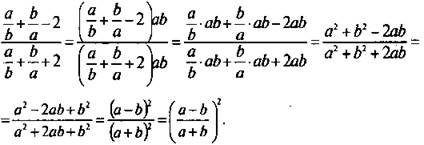
В выражениях, в которых повторяется одна и та же величина, удобно ввести новую переменную, обозначив ей повторяющуюся величину.

Пример 5

Упростим выражение:

Видно, что переменные х и у входят в этот пример только в виде суммы х2 + у2. Поэтому введем новую переменную а = х2 + у2 и для величин а и b запишем выражение. Имеем:

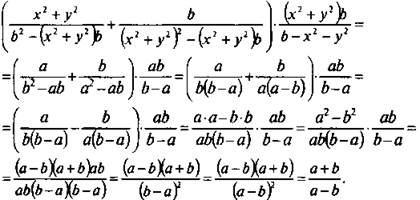
Теперь вернемся к старым переменным х и у и получим окончательный ответ:

IV. Задание на уроке

№ 147(б); 148 (а, б); 149(б); 150(б); 151 (а, б); 152 (а, б); 153 (a); 154 (г); 155 (б); 157 (а); 158 (б); 160 (б); 161 (б); 162 (е); 163 (в); 165 (а); 166 (б).

V. Задание на дом

№ 147 (а, в); 149 (а); 150 (а); 151 (в, г); 152 (в, г); 153 (б, д); 154 (б); 155 (а, в); 156 (б); 157 (б); 159 (а); 160 (а); 161 (а); 162 (д); 163 (г); 164 (б); 165 (б); 166 (а).

VI. Подведение итогов урока