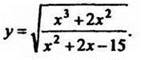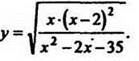Первообразная. Интеграл. Площадь криволинейной трапеции - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие

УРОК № 7

Тема. Первообразная. Интеграл. Площадь криволинейной трапеции

Цели: повторить определение первообразной, её основное свойство, три правила нахождения первообразных; рассмотреть применение формулы Ньютона-Лейбница для нахождения площади криволинейной трапеции.

Ход урока

I. Повторение пройденного материала

1. Сформулируйте определение первообразной.

2. Сформулируйте основное свойство первообразной.

3. Сформулируйте три правила нахождение первообразных.

4. Какую фигуру называют криволинейной трапецией? Запишите формулу для вычисления площади криволинейной трапеции.

5. Объясните, что такое интеграл.

6. Запишите формулу Ньютона-Лейбница.

II. Выполнение упражнений

1. Решить на стр. 297-298 № 268 и № 273.

2. Вычислить площадь фигуры, ограниченной параболами

Указание. Находим абсциссы точек пересечения графиков: Искомая площадь

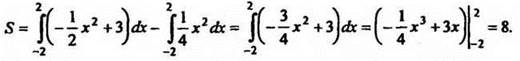
Ответ: 8.

3. Вычислить площадь фигуры, ограниченной линиями

Указание.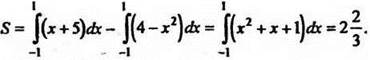

Ответ:

4. Найти площадь фигуры, ограниченной кривой , касательной к ней в точке х0 = 2 и осью абсцисс.

Решение

Составим уравнение касательной к графику функции в точке х0 = 2: уравнение касательной - уравнение касательной. Строим графики функций. Для того, чтобы найти искомую площадь, надо из площади ΔАВС вычесть площадь фигуры АВК:

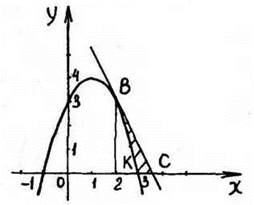
Рис. 58

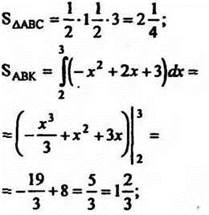
5. В каком отношении парабола у = х2 + 2 делит площадь четырёхугольника, вершины которого находятся в точках с координатами (0;0); (2;0); (0;6); (2;6)?

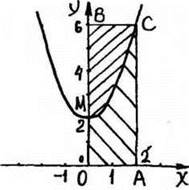
Рис. 59

Решение

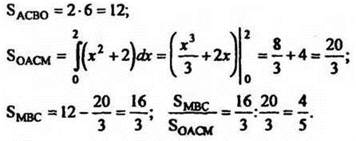
Ответ: 4:5 или 5:4.

6. Вычислить площадь фигуры, ограниченной линиями у = 4/x, y = х, х = 4.

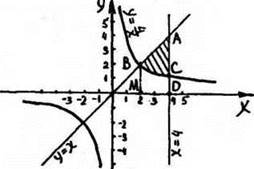
Рис. 60

Указание.

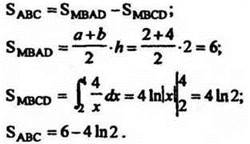
Ответ: 6 – 4ln2.

7. Вычислить площадь фигуры, ограниченной линиями у = 2х и у = 1,5x + 1.

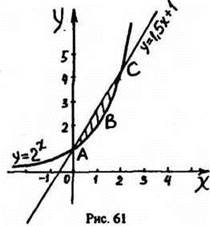
Указание.

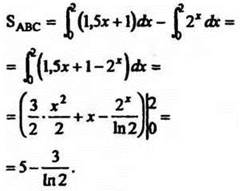
Ответ:

III. Итоги урока

IV. Домашняя контрольная работа

Вариант I	Вариант II
1. Решите уравнение 2. Найти площадь фигуры, ограниченной параболой касательной, проведённой через её вершину и осями координат. 3. Найти наибольшее и наименьшее значения функции на отрезке [-1;3]. 4. Найти область определения функции	1. Решите уравнение 2. Найти площадь фигуры, ограниченной параболой касательной, проведённой через её вершину и осью ординат. 3. Найти наибольшее и наименьшее значения функции на отрезке [0,2]. 4. Найти область определения функции