Алгебра и начала анализа для учащихся 11 класса поурочные планы
Наибольшее и наименьшее значения функции - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие
УРОК № 6
Тема. Наибольшее и наименьшее значения функции
Цели: повторить в ходе решения задач правило нахождения наибольшего и наименьшего значения функции; закрепить навык решения различных прикладных задач..
Ход урока
I. Проверочной работа (10-12 мин.
Вариант I .
Исследовать функцию и построить её график ![]()
Вариант II
Исследовать функцию и построить её график ![]()
II. Решение задач
1. Повторить правило нахождения наибольшего и наименьшего значения функции.
2. Найдите наибольшее и наименьшее значения функции ![]() на отрезке [-2; 0].
на отрезке [-2; 0].
Решение
Функция у(х) непрерывна на области определения х ≠ 1.
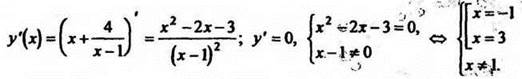
Критическая точка х = 3 не принадлежит отрезу [-2;0].
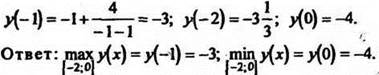
3. Найдите размеры участка прямоугольной формы, имеющего наименьший периметр, если его площадь равна 9 га.
Решение .
S = 9 га. = 90000 кв. м. Пусть стороны прямоугольника равны х м. и b м., тогда S = х · b = 90000, отсюда b = 90000/x, где х > 0.
Найдём периметр участка, ![]()
![]()
![]() не удовлетворяет условию x > 0.
не удовлетворяет условию x > 0.
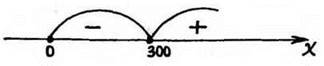
Рис. 54
Р'(х) < 0 на (0; 300); Р'(х) > 0 на (300;+∞). Значит, х = 300 является точкой минимума. При размерах участка 300 м и 300 м его периметр будет наименьшим. Ответ: 300 м и 300 м.
4. В основании пирамиды МАВС - прямоугольный треугольник, у которого АВ - гипотенуза. МА ![]() (ABC), АВ =
(ABC), АВ = ![]() м, МА = АС. Какова должна быть высота пирамиды, чтобы объем был наибольшим?
м, МА = АС. Какова должна быть высота пирамиды, чтобы объем был наибольшим?
Решение
Пусть ВС = х. Из ΔABC по теореме Пифагора найдем ![]()
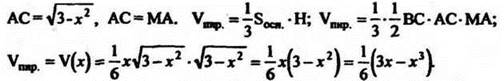
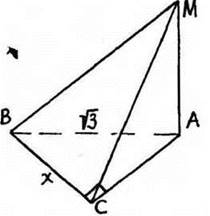
Рис. 55
По смыслу задачи 0 < х < > ![]() , т. к. ВС < АВ.
, т. к. ВС < АВ.
Исследуем функцию V(x) на (0;![]() ). На этом промежутке функция непрерывна и дифференцируема. Найдем критические точки функции:
). На этом промежутке функция непрерывна и дифференцируема. Найдем критические точки функции:
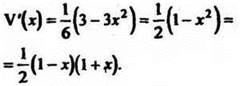
![]()

Рис. 56
При переходе через точку х = 1 знак производной изменяется с плюса на минус, следовательно, х = 1 есть точка максимума. Максимум функции в этой точке есть её наибольшее значение, т. к. в промежутке (0;![]() ) этот максимум единственный.
) этот максимум единственный.
![]() Объём пирамиды наибольший при высоте
Объём пирамиды наибольший при высоте ![]() м.
м.
Ответ: ![]() м.
м.
5. Периметр осевого сечения конуса равен 10 дм. Найти наибольший возможный объём этого конуса.
Решение
Пусть DC = х, тогда ВС = (5 - х). Из ΔBCD найдем
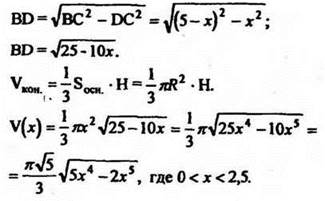
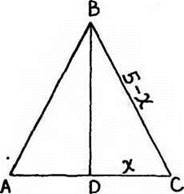
Рис. 57
Рассмотрим функцию ![]() Точка максимума V(x) является точкой максимума для f(x) в силу возрастания функции y =
Точка максимума V(x) является точкой максимума для f(x) в силу возрастания функции y = ![]() .
.
Найдём критические точки функции: ![]()
![]()
Функция f(x) непрерывна и дифференцируема на множестве всех действительных чисел; рассмотрим её на отрезке [0;2,5].
![]()
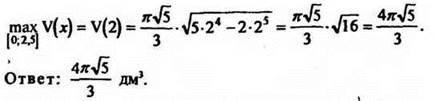
6. Самостоятельно: найти наибольшее значение функции ![]() на отрезке [-3;3]. Ответ: 1.
на отрезке [-3;3]. Ответ: 1.
III. Итоги урока
IV. Домашнее задание: повторить § 7 и § 8 темы «Первообразная» и «Интеграл»; решить на стр. 295 № 236, № 237 и № 242.