Алгебра и начала анализа для учащихся 11 класса поурочные планы
Решение тригонометрических уравнений и неравенств - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие
УРОК № 2
Тема. Решение тригонометрических уравнений и неравенств
Цели: повторить формулы для решения простейших тригонометрических уравнений и развивать навыки решения тригонометрических уравнений и неравенств.
Ход урока
I. Повторение пройденного материала
1. Решение уравнения cos t = а.
2. Уравнение sin t = а и его корни.
3. Уравнение tg t = а и уравнение ctg t = а.
4. Вспомнить решение простейших тригонометрических неравенств.
II. Решение тригонометрических уравнений и неравенств
1. Решить уравнение:
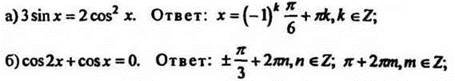
в) Найти все корни уравнения ![]() принадлежащие промежутку
принадлежащие промежутку ![]()
Указание. ![]()
Ответ: ![]()
2. Найти решения уравнения ![]() принадлежащие
принадлежащие ![]()
Решение
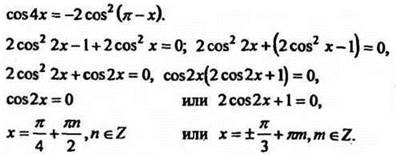
при n = 0, x1 = ![]() /4 принадлежит отрезку
/4 принадлежит отрезку ![]() при n = 1,
при n = 1, ![]() не принадлежит; при m = 0, х3 =
не принадлежит; при m = 0, х3 = ![]() /3 принадлежит; х4 = -
/3 принадлежит; х4 = -![]() /3 не принадлежит. Ответ:
/3 не принадлежит. Ответ: ![]() /4;
/4; ![]() /3.
/3.
3. Решить уравнение ![]()
Указание. После преобразований получим однородное уравнение ![]()
4. Решите уравнение ![]() Укажите один положительный и один отрицательный корни этого уравнения.
Укажите один положительный и один отрицательный корни этого уравнения.
Решение
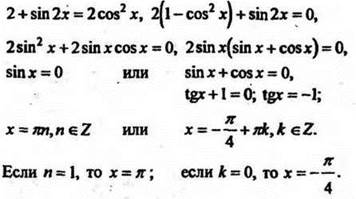
Ответ: отрицательный корень -![]() /4; положительный корень
/4; положительный корень ![]() ; корни уравнения
; корни уравнения ![]()
5. Решите уравнения:
![]()
Указание. ![]()
Ответ: ![]()
б) самостоятельно решить sin 2x + sin 4x = cos x.
Ответ: ![]()
6. Решить неравенство cos 3x < -0,5.
Решение
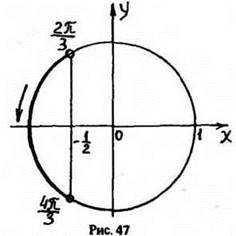
Пусть 3х = t, тогда cos t < -0,5.
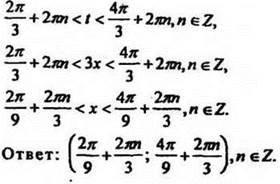
7*. Решить уравнение 7tg x + ctg x = 5sec х.
Решение
Уравнение определено при ![]() Приведем его к виду
Приведем его к виду ![]() Т. к. в области определения sinx cosx ≠ 0, то данное уравнение равносильно
Т. к. в области определения sinx cosx ≠ 0, то данное уравнение равносильно ![]() т. к.
т. к.
![]() решая эти уравнения, находим
решая эти уравнения, находим ![]()
Ответ ![]()
8*. Решить уравнение ![]()
Решение
Уравнение определено при x![]() (-∞;∞).
(-∞;∞).
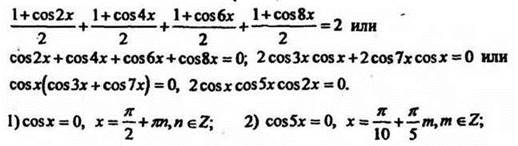
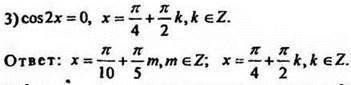
9. Самостоятельно решить неравенства на стр. 285 № 159.
III. Итоги урока
IV. Домашнее задание: повторить п. 8 - 11 из § 3; решить на стр. 285 № 154-157, № 160.