Алгебра и начала анализа для учащихся 11 класса поурочные планы
Решение тригонометрических уравнений и неравенств - урок 2 - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие
УРОК № 3
Тема. Решение тригонометрических уравнений и неравенств
Цели: закрепить решение тригонометрических уравнений и неравенств.
Ход урока
I. Проверка домашнего задания
1. На доске работают трое учащихся, решают: а) № 157 (б); 6) № 156 (г); в) №160 (б; в).
2. Еще один ученик решает на доске уравнение (остальные учащиеся в тетрадях):
Решение
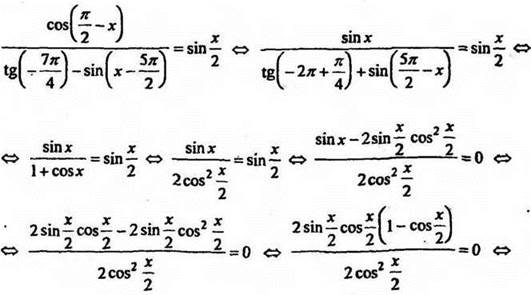
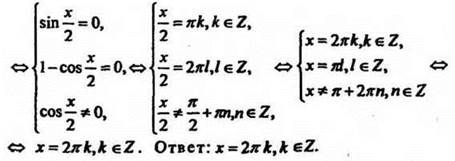
II. Выполнение упражнений
1. Объясняет учитель. Тригонометрические уравнения можно решать способом сравнения аргументов одноименных функций:
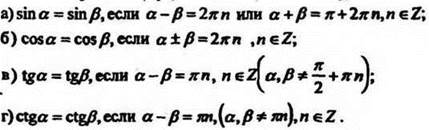
2. Решить уравнение ![]()
Решение
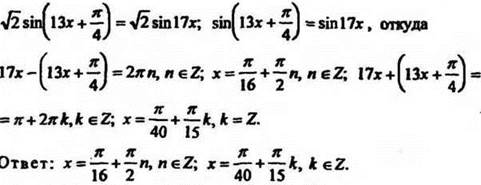
3. Решить уравнение ![]()
Решение
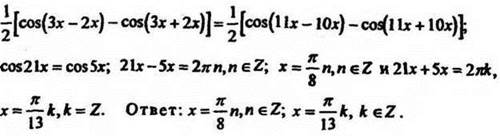
4. Решить уравнение ![]()
Решение
Уравнение определено при ![]()
Разделив обе части уравнения на ctg(x +1) ≠ 0, получим: ![]() откуда имеем
откуда имеем ![]()
5. Решить неравенство 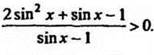
Решение
Данное неравенство равносильно ![]() при
при ![]() Учитывая, что |sin х| ≤ 1, установим знак неравенства:
Учитывая, что |sin х| ≤ 1, установим знак неравенства:
![]()
Рис. 48
Значит, ![]() откуда находим
откуда находим ![]()
Ответ: ![]()
6. Найдите в градусах наименьший положительный корень уравнения cos 8x = 1 - 3cos 4x. Ответ: 15°.
7. Найдите в градусах наибольший отрицательный корень уравнения ![]() Ответ: -45°.
Ответ: -45°.
8*. Решить уравнение ![]()
Решение
Применяя формулу 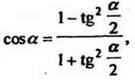 получим
получим 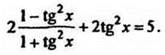
Полагая, tg2x = a, где a ≥ 0, имее.
![]()
Решая квадратное уравнение, получим а1 = 3; а2 = -1/2 (этот корень не подходит). Значит, tg2x = 3. Имеем два решения
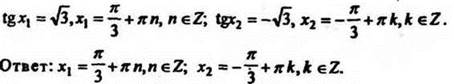
9*. Решить уравнение ![]()
Решение
Исходное уравнение эквивалентно системе
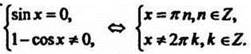
При n = 2k получаем, что ![]() n = 2
n = 2![]() k.
k.
Таким образом, подходят только ![]()
Ответ: ![]()
10. Решить уравнение 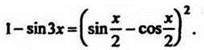
Ответ: ![]()
III. Итоги урока
IV. Домашнее задание: повторить § 4 и § 5 «Производная»; решить на стр. 94 (на отдельных листах) № 23, № 24 и № 25 и сдать.