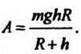рассмотреть упражнения на нахождение объёмов тел фигур вращения - ПРИМЕНЕНИЕ ИНТЕГРАЛА - ИНТЕГРАЛ - 1-е полугодие

Цели: рассмотреть упражнения на нахождение объёмов тел фигур вращения.

Ход урока

I. Проверка домашнего задани.

II. Решение упражнений

1. № 370 (a); № 371 (в).

№ 370(a). Сначала находим пределы интегрирования из уравнения 1 - х2 = 0 н вычисляем по формуле нужный объём:

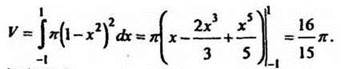
№ 371 (в)

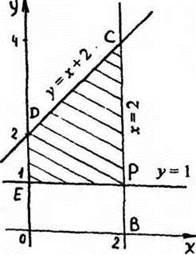
Рис. 16

Решение

V = V1 – V2, где V1 - объём тела, полученного при вращении криволинейной трапеции OBCD, а V2 - объём тела, полученного при вращении прямоугольника ОВРЕ вокруг оси абсцисс.

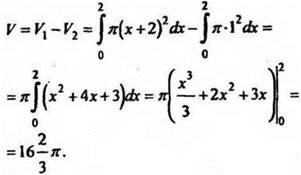
2. № 370 (б); № 371 (г) - самостоятельно. №370(6).

Решение

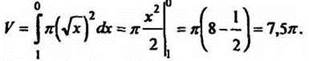
№ 371 (г).

Решение

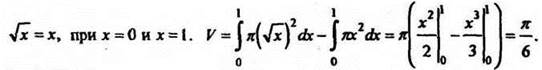
3. № 372 (б).

Решение

Данное тело можно рассматривать как тело, полученное при вращении вокруг оси абсцисс криволинейной трапеции, ограниченной линиями

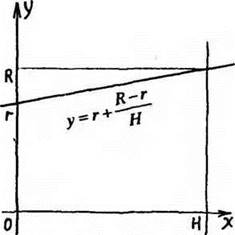
Рис. 17

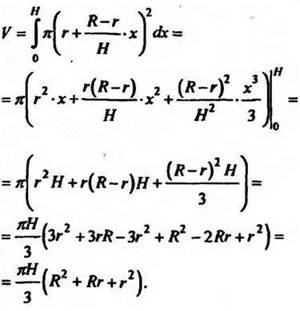
III. Рассмотреть наиболее удачные примеры применения интеграла, предложенные учащимися

IV. Итоги урока

V. Домашнее задание: Подготовиться к зачёту по теме «Первообразная и интеграл» (вопросы с. 199) и к контрольной работе по теме «Интеграл».

По желанию.

Задачи:

1. Сила упругости пружины с закрепленным одним концом пропорциональна отклонению другого конца пружины на 10 см. Какую работу надо совершить для того, чтобы растянуть пружину на 25 см?

Решение

Обозначим величину растяжения пружины через х. Тогда сила упругости её будет равна F(x) = kx. Т. к. F(10) = 350, то к = 350/10 = 35. Таким образом, F(x) = 35х. Тогда работа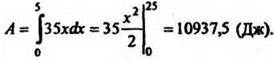

2. Какую работу требуется выполнить, чтобы с помощью ракеты тело массой m поднять с поверхности Земли, радиус которой R, на высоту h.

Решение

На тело массой m по закону всемирного тяготения действует сила где М - масса Земли, а r - расстояние тела от центра Земли. Поэтому 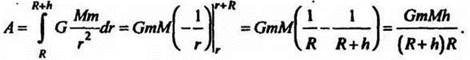На поверхности Земли, т. e. при r = R, имеем F = mg, т. e. 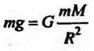и 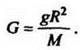Отсюда