РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ ПОНЯТИЕ ДВИЖЕНИЯ. ОСЕВАЯ И ЦЕНТРАЛЬНАЯ СИММЕТРИИ - ДВИЖЕНИЯ

Цель деятельности учителя

Создать условия для закрепления теоретических знаний по изученной теме

Термины и понятия

Отображение плоскости на себя, движение, осевая симметрия, центральная симметрия

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют объснять, что такое отображение плоскости на себя; знают понятие движения и умеют применять при решении задач

Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации.

Регулятивные: понимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве, умеют формулировать, аргументировать и отстаивать свое мнение.

Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Задания для самостоятельной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Сформировать уровень теоретических знаний

(Ф)

1. Опрос по теории: вопросы 7-13 (с. 297).

2. Проверка домашнего задания

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Научить применять полученные знания при решении задач

(Ф/И)

1. Разобрать с учащимися решение задачи № 1157.

2. Провести самостоятельную работу.

Вариант I

1. Дан четырехугольник ABCD. Постройте фигуру, симметричную данной:

а) относительно вершины D.

б) относительно диагонали АС.

2. Докажите, что при движении квадрат отображается на квадрат.

Вариант II

1. Дан четырехугольник ABCD. Постройте фигуру, симметричную данной:

а) относительно вершины А.

б) относительно диагонали BD.

2. Докажите, что при движении прямоугольник отображается на прямоугольник

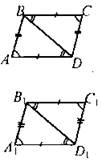
№ 1157.

Дано: ABCD и A₁B₁C₁D₁ — параллелограммы;

Доказать: .

Доказательство:

(накрест лежащие), то есть ∆ABD = ∆BDC (по признаку).

Аналогично: так как (по признаку).

Получаем, что значит,

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Сделайте вывод по результатам урока.

- Задайте три вопроса по уроку.

- Оцените свою работу на уроке

(И) Домашнее задание: решить № 1155, 1156, 1160, 1161