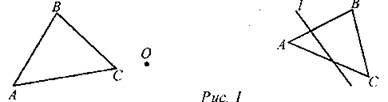Геометрия 9 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
СВОЙСТВА ДВИЖЕНИЙ - ДВИЖЕНИЯ
|
Цель деятельности учителя |
Создать условия для рассмотрения свойств движений |
||
|
Термины и понятия |
Отображение плоскости на себя, движение, осевая симметрия, центральная симметрия |
||
|
Планируемые результаты |
|||
|
Предметные умения |
Универсальные учебные действия |
||
|
Умеют объснять, что такое отображение плоскости на себя; знают, что такое движение |
Познавательные: умеют понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации; осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий, классификации. Регулятивные: понимают и принимают цели и задачи учебной деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют способность к эмоциональному восприятию математических объектов, задач, решений, рассуждений |
||
|
Организация пространства |
|||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||
|
Образовательные ресурсы______ |
• Задания для индивидуальной и фронтальной работы |
||
|
I этап. Актуализация опорных знаний учащихся |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Проверить уровень теоретических знаний |
(Ф) 1. Теоретический опрос. - Сформулируйте определение отображения плоскости на себя. - Приведите примеры отображения плоскости на себя. -Докажите, что осевая и центральная симметрии являются отображением плоскости на себя. - Что такое движение? - Являются ли осевая и центральная симметрии движениями? 2. Двое учащихся вызываются к доске: один строит фигуру, симметричную данной относительно точки О; второй - относительно прямой l.
|
||
|
II этап. Учебно-познавательная деятельность |
|||
|
Цель деятельности |
Совместная деятельность |
||
|
Рассмотреть свойства движения |
(Ф) Доказать, чтр осевая и центральная симметрии являются движениями. После этого рассмотреть теорему о том, что при движении отрезок отображается на отрезок, и следствие из нее. В ходе доказательства теоремы обратить внимание учащихся на то, что доказательство состоит из двух частей: во-первых, доказывается, что каждая точка Р данного отрезка MN отображается в некоторую точку Р1 отрезка M1N1, и, во-вторых, что в каждую точку Р1 отрезка M1N1 переходит какая-то точка Р данного отрезка MN. (И) Задание для учащихся: выяснить, в какую фигуру при движении отображается треугольник, и доказать справедливость своего утверждения. Ответ: при движении треугольник отображается на равный ему треугольник |
||
|
III этап. Закрепление изученного материала |
|||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|
|
Научить применять свойства движений при решении задач |
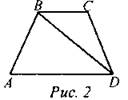
(Ф/И) 1) На доске и в тетради решить № 1152 (б). 2) Решить самостоятельно № 1152 (в) и 1158 |
№ 1152 (б).
Решение: При движении отрезок отображается в отрезок, треугольник - на равный ему треугольник, угол - на равный ему угол. Используя эти свойства движений, можно получить различные способы решений:
|
|
|
IV этап. Итоги урока. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
||
|
(Ф/И) - Составьте синквейн к уроку |
(И) Домашнее задание: решить № 1153, 1159 |
||