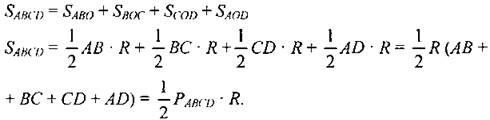СВОЙСТВО ОПИСАННОГО ЧЕТЫРЕХУГОЛЬНИКА - ОКРУЖНОСТЬ

Цель деятельности учителя

Создать условия для выведения свойства описанного четырехугольника и совершенствовать навыки решения задач с использованием свойства описанного четырехугольника

Термины и понятия

Окружность, вписанная в четырехугольник; описанный четырехугольник

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам содержания

Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: формулируют, аргументируют и отстаивают свое мнение.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Задания для индивидуальной работы

Проверить выполнение домашнего задания

(И) 1. Тест с последующей самопроверкой (см. Ресурсный материал).

2. Вызываются несколько учеников, которые на доске показывают решение домашних задач

II этап. Мотивация к изучению новой темы

Цель деятельности

Постановка учебной задачи

Совершенствовать навыки решения задач на готовых чертежах

(Ф/И) Решить устно.

Найти: радиус окружности, вписанной в треугольник со сторонами 10 см, 10 см, 12 см.

Ответ: R = 3 см.

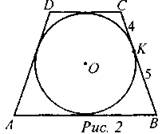
Дано: ABCD - равнобедренная трапеция.

Найти: DC и АВ.

Ответ: DC = 8, АВ = 10

III этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Рассмотреть свойство описанного четырехугольника

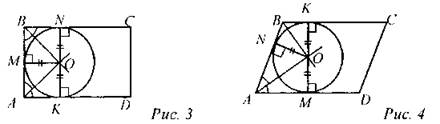
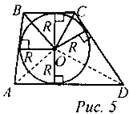
(Ф/И) 1. Объяснить, что не во всякий четырехугольник можно вписать окружность, на примерах: а) прямоугольника (рис. 3); б) параллелограмма (рис. 4).

2. Сформулировать свойство описанного четырехугольника и предложить учащимся доказать его самостоятельно, а затем заслушать и обсудить варианты доказательств.

Теорема. В любом описанном четырехугольнике суммы противоположных сторон равны.

3. Задание для учащихся: сформулировать утверждение, обратное свойству описанного четырехугольника, и выяснить его справедливость (см. задачу № 724)

IV этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(Ф) 1. На доске и в тетради разобрать решение задачи № 697.

(И) 2. Провести самостоятельную работу обучающего характера.

Вариант I

1. В равносторонний треугольник вписана окружность радиусом 4 см. Найдите сторону треугольника.

2. Четырехугольник ABCD описан около окружности. Найдите стороны АВ и CD, если ВС = 6 см, AD = 9 см, АВ в два раза больше, чем CD.

Вариант II

1. В равносторонний треугольник со стороной 8 см вписана окружность. Найдите радиус окружности.

2. Четырехугольник ABCD описан около окружности. Найдите стороны ВС и AD, если АВ = 1 см, CD = 11 см, ВС в 2 раза меньше AD

№ 697.

Дано: ABCD - описанный четырехугольник.

Доказать:

Доказательство:

Самостоятельная работа

Вариант I

1. 8√3 см.

2. АВ = 10 см, CD = 5 см.

Вариант II

1. 4√3/3 см.

2. ВС = 6 см, AD = 12 см

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Закончите предложения.

• Чтобы в четырехугольник вписать окружность...

• Чтобы найти площадь описанного четыреугольника...

- Оцените свою работу

(И) Домашнее задание: № 696, 697, 698

Ответы к тесту

1

2

3

4

Вариант I

б

а

в

а

Вариант II

а

б

а

в