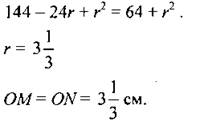Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ВПИСАННАЯ ОКРУЖНОСТЬ - ОКРУЖНОСТЬ
|
Цель деятельности учителя |
Создать условия для введения понятий вписанной и описанной окружностей, доказательства теоремы об окружности, вписанной в треугольник |
||||
|
Термины и понятия |
Окружность, вписанная в треугольник |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Владеют базовым понятийным аппаратом по основным разделам содержания |
Познавательные: осознанно владеют логическими действиями определения понятий, обобщения, установления аналогий; умеют применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач. Регулятивные: принимают и сохраняют цели и задачи учебной деятельности. Коммуникативные: умеют формулировать, аргументировать и отстаивать свое мнение. Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||
|
Образовательные ресурсы |
• Учебник. • Задания для индивидуальной работы |
||||
|
I этап. Актуализация опорных знаний учащихся |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Проверить выполнение домашнего задания |
(Ф/И). Анализ домашней проверочной работы. Ответы к задачам проверочной работы: Вариант I 1. 48°. 2. 30 см2. Вариант II 1. 5. 2. 20 см2 |
||||
|
II этап. Мотивация к деятельности |
|||||
|
Цель деятельности |
Постановка учебной задачи |
||||
|
Совершенствовать навык решения задач с целью подготовки к восприятию нового материала |
(Ф/И). Решение задач на готовых чертежах.
Дано: АВ, АС - касательные, В, С - точки касания. ∠BAC = 56°, ОС = 4 см. Найти: ∠OAB, ОВ.
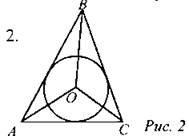
Дано: АВ, ВС, АС - касательные, ∠BOC = 120°, ∠ABO = 25°, ∠AOC = 115°. Найти: углы треугольника АОВ. Доказать: О - точка пересечения биссектрис ∆AВС |
||||
|
III этап. Изучение новой темы |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Ввести понятие вписанной окружности и доказать теорему о вписанной окружности |
(Ф) Материал предлагается учителем в виде лекции. 1. Ввести понятие окружности, вписанной в многоугольник. Определение. Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник - описанным около этой окружности.
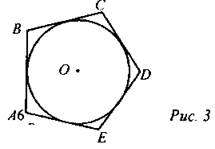
ABCDE — описанный около окружности с центром О пятиугольник. Окружность с центром О вписана в пятиугольник ABCDE. АВ, ВС, CD, DE, АЕ касаются окружности.
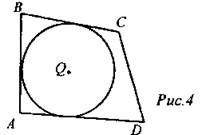
Окружность с центром Q не вписана в четырехугольник ABCD, так как CD не касается окружности. 2. Формулировка и доказательство теоремы об окружности, вписанной в треугольник. Теорема. В любой треугольник можно вписать окружность. Для доказательства теоремы можно предложить учащимся самостоятельно решить задачу на построение, а затем обсудить варианты решений |
||||
|
IV этап. Закрепление изученного материала |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Совершенствовать навыки решения задач |
(Ф/И) Выполнить № 701 (для остроугольного треугольника), 689, 691 |
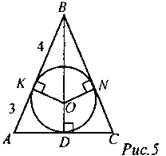
№ 691.
Краткое решение: Так как АВ, ВС, АС - касательные, K, N, D -точки касания, то АК = AD,CD = CN, ВК = BN. Так как AB = BC, тo CN =CD = 3 см => РABC = 3 ∙ 4 + 4 ∙ 2 = 20 см. Ответ: 20 см. № 689.
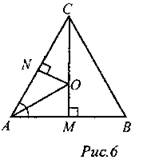
Решение: 1) Центр О вписанной окружности искомого радиуса r лежит на биссектрисе СМ треугольника АВС, а так как CM ⊥ АВ, то вписанная окружность касается отрезка АВ в точке М. Поэтому ОМ = r. Обсудить с учащимися различные способы решения Рис.6 этой задачи. Способ 1. 1) АМ = 1/2АВ = 5 см. 2) М и N - точки касания, следовательно, AN = AM =5 см, откуда CN = АС – AN= 8 см. 3) В ∆АСМ: 4) В ∆CON: СО2 = CN2 +ON2, то есть (12 - r)2 = 82+ r2;
Способ 2. 1) В ∆ACM: AM = 1/2АВ = 5 см.
2) Отрезок АО - биссектриса треугольника АМС (так как О - центр вписанной окружности), поэтому
|
|||
|
V этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И). - Задайте три вопроса по изученной теме. - Оцените свою работу |
(И) Домашнее задание: вопросы 21, 22, с. 188; № 701 (для прямоугольного и тупоугольного треугольников), 690, 693 (а, б) |
||||