ТЕОРЕМА О ТОЧКЕ ПЕРЕСЕЧЕНИЯ ВЫСОТ ТРЕУГОЛЬНИКА - ОКРУЖНОСТЬ

Цель деятельности

Создать условия для рассмотрения теоремы о точке пересечения высот треугольника и показать ее применение при решении

учителя

задач

Термины и понятия

Высота треугольника, точка пересечения высот треугольника

Планируемые результаты

Предметные умения

Универсальные учебные действия

Имеют систематические знания о плоских фигурах и их

Познавательные: умеют понимать и использовать математические средства наглядности для иллюстрации, интерпретации, аргументации; применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

Регулятивные: принимают и сохраняют учебные задачи.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

свойствах

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная

(И)

Образовательные

ресурсы

• Учебник.

• Задания для фронтальной, индивидуальной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Проверить выполнение домашней работы

(Ф) Решить устно.

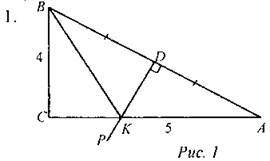
Найти: Р_BKC, Р_АВС.

Решение:

1) В ∆АВК DK - серединный перпендикуляр => ВК = АК = 5.

2) ∆ВСК - египетский => СК = 3.

3) CP = KD = 3 => DA = BD = 4.

4) Р_BKC = 3 + 4 + 5 = 12, Р_АВС = 4 + 8 + 8 = 20.

Ответ: 12, 20.

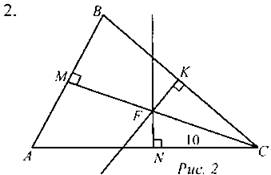
Дано: FK, FN серединные перпендикуляры. АВ = 16, CF = 10.

Найти: расстояние от точки F до стороны АВ.

Решение:

1. FK, FN серединные перпендикуляры => МС также серединный перпендикуляр => АМ = ВМ = 8.

2. FC = 10 => FB = AF = 10.

3. В ∆MFA: FA = 10, АМ = 8 => MF = 6.

Ответ: 6.

II этап. Мотивация изучения новой темы

Цель деятельности

Постановка учебной задачи

Доказать теорему о точке пересечения высот треугольника

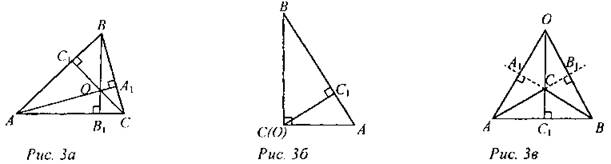
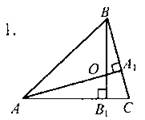
(Ф)

— Какие элементы треугольника пересекаются в одной точке? (Биссектрисы треугольника, серединные перпендикуляры к сторонам треугольника, медианы треугольника.)

— В каком треугольнике совпадают точка пересечения биссектрис, точка пересечения медиан, точка пересечения серединных перпендикуляров? (В равностороннем.)

— Как вы думаете, пересекаются ли высоты треугольника в одной точке? (Варианты ответов: а) да; б) только в остроугольном; в) в остроугольном и прямоугольном.)

В ходе обсуждения выполнить рис. 3 (а, б, в).

О - точка пересечения высот ∆АВС или их продолжений.

1. Сформулировать и доказать теорему о точке пересечения высот треугольника.

Теорема. Высоты треугольника (или их продолжения) пересекаются в одной точке. (Доказать может сам учитель; можно предложить учащимся разобрать самостоятельно.)

2. Ввести понятие четырех замечательных точек треугольника.

Четыре замечательные точки треугольника:

1) Точка пересечения медиан треугольника.

2) Точка пересечения биссектрис треугольника.

3) Точка пересечения серединных перпендикуляров.

4) Точка пересечения высот треугольника

III этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Применение теоремы при решении задач

(Ф/И)

1. Решить № 683 и 685 у доски и в тетрадях.

2. Решить № 684, 688

№ 683.

Дано: ∆AВС, АВ ≠ АС, AM - медиана.

Доказать: AM не ⊥ ВС.

Доказательство:

1) Примем AM ⊥ ВС, следовательно, получим: ∆АМС и ∆АМВ; AM - общая, СМ = МВ (по условию), следовательно, ∆АМС = ∆АМВ (по двум катетам), следовательно, АС = АВ, что противоречит условию АВ ≠ АС.

2) Значит, наше предположение неверно, а верно AM не ⊥ ВС, что и требовалось доказать.

№ 685.

Дано: ∆АВС, АА₁ ∩ ВВ₁ = М, АС = ВС, ВВ₁⊥ АС, АА₁⊥ ВС.

Доказать: CM ⊥ BA, ВК = КА.

Доказательство:

1) Так как АА₁∩ ВВ₁ = М, то СМ ⊥ АВ (замечательное свойство треугольника).

2) ∆ВСК и ∆АСК: СК - общая, ВС = АС (по условию), следовательно, ∆ВСК = ∆АСК (по катету и гипотенузе), следовательно, ВК = КА, что и требовалось доказать.

№ 684.

Краткое решение:

Биссектрисы углов треугольника пересекаются в одной точке, следовательно, СМ - биссектриса ∠ACB. Пусть СМ ∩ АВ = D. Тогда CD - биссектриса, проведенная к основанию равнобедренного треугольника => CD - высота, то есть CD ⊥ АВ, значит, СМ ⊥ АВ.

№ 688.

Построение:

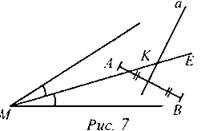
1) Построить биссектрису ME угла М.

2) Построить серединный перпендикуляр к отрезку АВ - прямую а.

3) а ∩ ME = К. К - искомая точка

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Назовите четыре замечательные точки треугольника.

- Оцените свою работу

(И) Домашнее задание.

Вариант I

Дано: ∠CAB = 42°.

Найти: ∠ACO.

2. В треугольнике MNK биссектрисы пересекаются в точке О. Расстояние от точки О до стороны MN = 6 см, NK = 10 см. Найдите площадь треугольника NOK.

Вариант II

Найти: расстояние от точки О до стороны АС.

2. В треугольнике MNK медианы МР и NE пересекаются в точке О и равны 12 и 15 см соответственно. Найдите площадь треугольника МОЕ, если МР ⊥ NE