СЕРЕДИННЫЙ ПЕРПЕНДИКУЛЯР - ОКРУЖНОСТЬ

Цель деятельности учителя

Создать условия для введения понятия серединного перпендикуляра и рассмотрения теоремы о серединном перпендикуляре; показать применение теоремы о серединном перпендикуляре при решении задач

Термины и понятия

Серединный перпендикуляр, равноудаленность

Планируемые результаты

Предметные умения

Универсальные учебные действия

Имеют систематические знания о плоских фигурах и их свойствах

Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач, применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); парная (П); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для парной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Проверить домашнее задание

(Ф) Теоретический опрос.

1) Сформулировать и доказать теорему о биссектрисе угла.

2) Сформулировать и доказать теорему, обратную теореме о биссектрисе угла.

3) Сформулировать и доказать следствие из теоремы о биссектрисе угла

II этап. Мотивация к деятельности

Цель деятельности

Постановка учебной задачи

Совершенствовать навык решения задач по готовым чертежам с целью подготовки учащихся к восприятию нового материала

(П)

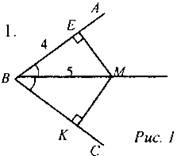
Дано: BE = 4, ВМ = 5.

Найти: МК.

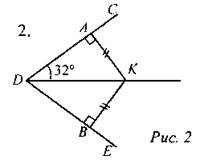
Найти: ∠ADB.

Дано: АВ = ВС.

Доказать: ВМ ⊥ АС.

(Ф) № 677.

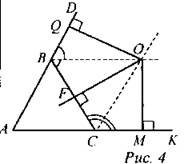
Дано: ∆АВС; ВО, СО - биссектрисы.

Доказать: О - центр окружности; АВ, АС и ВС - ее касательные.

Доказательство:

1) Так как ВО - биссектриса ∠CBD, то OQ ⊥ BD и OF ⊥ ВС равны по свойству биссектрисы угла.

2) Так как СО - биссектриса ∠BCK, то OF ⊥ ВС и ОМ ⊥ СК равны по свойству биссектрисы угла.

3) Вывод: OQ = OF (из п. 1), OF = ОМ (из п. 2), следовательно, OQ = OF = ОМ - радиусы окружности с центром в точке О, а АВ, ВС, АС - касательные (по определению)

III этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятие серединного перпендикуляра и доказать сопутствующую теорему

(Ф)

1. Ввести понятие серединного перпендикуляра, используя Picture на доске.

2. Доказать теорему о свойстве серединного перпендикуляра.

3. Доказать следствие из этой теоремы.

(Доказательство теоремы о серединном перпендикуляре к отрезку и следствия из нее желательно изложить учителю.)

IV этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(Ф) Решить № 679 (б), 680, 682

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Какое новое понятие узнали на уроке?

- Сформулируйте 3 вопроса по сегодняшней теме

(И) Домашнее задание: 679 (а), 681, 686 (решена в учебнике)