СВОЙСТВО БИССЕКТРИСЫ УГЛА - ОКРУЖНОСТЬ

Цель деятельности учителя

Создать условия для рассмотрения свойства биссектрисы угла и показать его применение при решении задач

Термины и понятия

Угол, биссектриса угла, равноудаленность

Планируемые результаты

Предметные умения

Универсальные учебные действия

Имеют систематические знания о плоских фигурах и их свойствах

Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач; применять индуктивные и дедуктивные способы рассуждений, видеть различные стратегии решения задач.

Регулятивные: принимают и сохраняют учебные задачи.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Составить план решения тех задач, с которыми учащиеся не справились в самостоятельной работе

(Ф)

1. Анализ ошибок, допущенных в самостоятельной работе.

1) Сообщить общие замечания и рекомендации по решению задач самостоятельной работы.

2) Составить план решения задач, с которыми не справилось большинство учащихся.

2. Проверка выполнения домашнего задания (№ 661, 663).

№ 661.

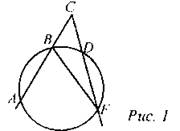
Дано: АС, FC - секущие, AF = 140°, BD = 52°.

Найти: ∠ACF.

Решение:

1) ∠ABF - вписанный, значит,

2) ∠BFD - вписанный, значит,

3) В ∆BCF: ∠F = 26°, ∠B = 180° - 70° = 110° (как смежный с ∠ABF), ∠C = 180° - (110° + 26°) = 44°.

Ответ: 44°.

№ 663.

Дано: АС - диаметр, Окр (O; R), AB - хорда, AM - касательная, ∠MAB < 90°.

Доказать: ∠MAB = ∠ACB.

Доказательство:

1) ∆АВС - прямоугольный, так как

2) Так как AM - касательная к окружности, то AM ⊥ АС, то есть ∠MAB = 90° - ∠BAC (**).

3) Сравним (*) и (**), получим: ∠C = ∠MAB, что и требовалось доказать

II этап. Мотивация к деятельности

Цель деятельности

Постановка учебной задачи

Совершенствовать навык решения задач по готовым чертежам с целью подготовки учащихся к восприятию нового материала

(Ф/И).

1. Доказать: ВС = DC (рис. 3).

2. Доказать: точка М равноудалена от точек А и В (рис. 4).

3. Доказать: АС - биссектриса ∠BAD (рис. 5)

III этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Рассмотреть теорему о свойстве биссектрисы угла и ее следствие

(Ф)

1. Доказательство теоремы.

2. Доказательство следствия из теоремы.

Изложить доказательства лучше самому учителю в виде небольшой лекции

IV этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

(Ф/И)

Решить № 674, 675, 676 (а)

№ 674.

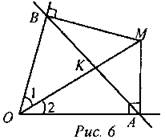
Дано: ∠О, ОМ - биссектриса, МА ⊥ ОА, МВ ⊥ ОВ.

Доказать: АВ ⊥ ОМ.

Доказательство:

1) Рассмотрим ∆МОВ и ∆МОА: ОМ - общая, ∠1 = ∠2 (по условию), следовательно, ∆МОВ = ∆МОА (по гипотенузе и острому углу). Значит, ОВ = ОА, следовательно, ∆АОВ - равнобедренный.

2) Рассмотрим ∆ОВК и ∆OAK: ОВ = ОА (из п. 1), ∠1 = ∠2 (по условию), ОК - общая, следовательно, ∆ОВК = ∆OAK (по двум сторонам и углу между ними), следовательно, ВК = КА, значит, ОК - медиана, тогда OK ⊥ ВА (свойство медианы равнобедренного треугольника), что и требовалось доказать.

№ 675.

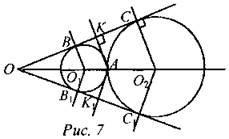
Дано: ∠О, Окр. (O₁; R) ∩ Окр. (O₂, r) = А.

Доказать: О₁, О₂ є ОА.

Доказательство:

1) Так как ВС и В₁С₁ - касательные к окружностям, то O₁В ⊥ ВС, O₂С ⊥ ВС и O₁В₁⊥ В₁С₁, O₂С₁⊥ В₁С₁. Значит, точки O₁ и O₂ лежат на биссектрисе ∠О - свойство биссектрисы угла.

2) А лежит на биссектрисе, так как АК = АК₁ (свойство биссектрисы), что и требовалось доказать.

№ 676 (а).

Краткое решение:

ОВ = ОС = r = 5 см, ОВ ⊥ АВ, ОС ⊥ АС пo свойству касательной. Таким образом, АО - биссектриса ∠ВАС, то есть∠1 = ∠2 = 30°. Следовательно, АО = 20В = 10 (см).

Ответ: 10 см

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Что нового узнали о биссектрисе угла?

- Составьте синквейн к уроку

(И) Домашнее задание: вопросы 15, 16, с. 187; № 676 (б), 778 (а)