РЕШЕНИЕ ЗАДАЧ ПО ТЕМЕ «ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ» - ОКРУЖНОСТЬ

Цель деятельности учителя

Создать условия для систематизации теоретических знаний по теме “Центральные и вписанные углы”

Термины и понятия

Окружность, хорда, радиус, диаметр, дуга; хорда, стягивающая дугу окружности; вписанный угол

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют работать с геометрическим текстом, точно и грамотно излагать свои мысли в устной и письменной речи

Познавательные: умеют создавать, применять и преобразовывать знаково-символические средства, модели и схемы для решения учебных задач.

Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения учебных математических задач.

Коммуникативные: умеют организовывать учебное сотрудничество и совместную деятельность с учителем и сверстниками, работать в группах.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Актуализация опорных знаний учащихся

Цель деятельности

Совместная деятельность

Проверить правильность выполнения домашнего задания

(Ф/И) К доске вызываются 2 ученика: первый готовит доказательство теоремы; второй - решение задачи № 667.

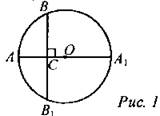
Дано: А₁А - диаметр, АА₁⊥ ВВ₁, АА₁∩ ВВ₁ = О, АС = 4 см, СА₁ = 8 см.

Найти: ВВ₁.

Решение:

1) Так как АА₁⊥ ВВ₁, то ОС является высотой равнобедренного ABOBi, а значит, ОС - медиана, то есть ВС = СВ₁.

2) По свойству хорд: Отсюда ВВ₁ = 4√2

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач

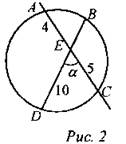
(Ф/И)

1. Решить задачу № 669.

2. Решить задачи по готовым чертежам.

Найти: BE и α.

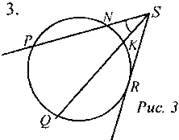
Дано: SN = 4SP = 9SK = 3

Найти: SR, SQ, а.

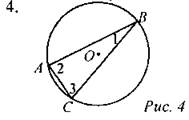
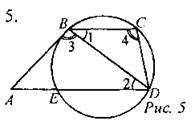
Дано: ∪АС : ∪AB : ∪СВ = 3 : 7 : 8

Найти: ∠1, ∠2, ∠3.

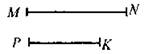
Построить отрезок

Построение:

а) на прямой построить отрезок АВ, равный сумме длин отрезков MN и РК;

б) построить середину отрезка АВ - точку О;

в) построить окружность с центром в точке О и радиусом, равным АО;

г) построить перпендикуляр к отрезку АВ через точку Q, лежащую на отрезке АВ так, что AQ = MN, BQ= РК;

д) построить точку пересечения данного перпендикуляра с построенной окружностью - точку Е; отрезок QE - искомый.

2. После решения задачи обратить внимание: угол, вершина которого лежит внутри круга, измеряется полусуммой двух дуг, одна из которых заключена между его сторонами, а другая - между продолжениями сторон.

3. После решения задачи обратить внимание: угол, вершина которого лежит вне круга, измеряется полуразностью двух дуг, заключенных между его сторонами,

4. Решение:

значит,

5. Окружность проходит через вершины В, С, D трапеции ABCD (AD и ВС - основания) и касается стороны АВ в точке В.

Докажите, что

Решение:

1) Так как ВС || AD, то ∠1 = ∠2.

2) значит, ∠3 = ∠4.

3) ∆ABD ~ ∆BCD (по двум углам)

III этап. Самостоятельная работа

Цель деятельности

Задания для самостоятельной работы

Совершенствовать навыки самостоятельной работы, самопроверки и самоконтроля

(И)

Вариант I

Дано: ∪AB : ∪АС = 3 : 2, ∠A = 50°.

Найти: ∠B, ∠C, ∠BOC.

2. Хорды AB и CD пересекаются в точке Е. Найдите CD, если АЕ = 4 см, BE = 9 см, а длина СЕ в четыре раза больше длины DE.

Вариант II

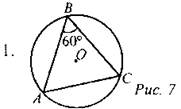
Дано: ∠В = 60°, ∪АВ : ∪ВС = 7 : 5.

Найти: ∠A, ∠C, ∠AOC.

2. Хорды MN и КР пересекаются в точке Т. Найдите BN, если АТ = 6 см, РТ = 8 см, а длина МТ в три раза меньше длины NT

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою работу на уроке

(И) Домашнее задание: № 661, 663