ЗАДАЧИ НА ПОСТРОЕНИЕ МЕТОДОМ ПОДОБИЯ - Урок 2 - ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для применения подобия треугольников в задачах на построение

Термины и понятия

Пропорциональные отрезки, отношение, пропорции, среднее пропорциональное

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют навыками устных, письменных, инструментальных вычислений, построений

Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации в других дисциплинах, в окружающей жизни.

Регулятивные: умеют адекватно оценивать правильность или ошибочность решения учебной задачи.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.

Личностные: проявляют креативность мышления, инициативность, находчивость, активность при решении геометрических задач

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Учебник.

• Задания для групповой и индивидуальной работы

I этап. Активизация знаний учащихся

Цель деятельности

Совместная деятельность

Выявить трудности в выполнении домашнего задания

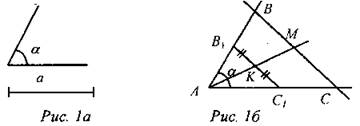
(Ф/И)

1. Проверка домашнего задания.

№ 588.

Дано: ∠А = α, АМ = а (медиана), АВ : АС = 2 : 3 (рис. 1а).

Построить: ∆АВС.

Построение:

Построение (рис 16):

1) ∠A = α.

2) Построить на сторонах ∠A отрезки АВ₁ и АС₁ так, что АВ₁ : АС₁ = 2 : 3 (АВ₁ = 2 см, АС₁ = 3 см).

3) Отметить середину В₁С₁ - точку К. АК - медиана ∆АВ₁С₁.

4) На луче АК отложить отрезок AM, равный α.

5) Через точку А провести прямую ВС || В₁С₁. ∆АВС - искомый

II этап. Решение задач

Цель деятельности

Совместная деятельность

Совершенствовать навыки решения задач методом подобия

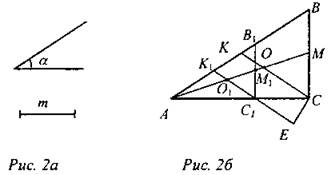
(Г)

Каждую из задач учащиеся решают самостоятельно в группах, а затем идет обсуждение решения, выбор наиболее рационального способа.

1. Построить треугольник АВС по углу А, отношению сторон АВ : АС = 2 : 1 и расстоянию от точки пересечения медиан до вершины С.

Дано: ∠A = α, О - точка пересечения медиан ААВС, ОС = т, АВ : АС = 2 : 1.

Построить: ∆АВС.

Построение:

а) Построить угол А, равный α.

б) На сторонах угла А отложить отрезки АС₁ и АВ₁ так, что АВ₁ : АС₁ = 2 : 1.

в) Построить точку пересечения медиан треугольника АВ₁С₁ - точку O₁.

г) На луче O₁С₁ отложить отрезок O₁Е, равный m.

д) Построить прямую ЕС, параллельную медиане АМ₁ треугольника АВ₁С₁, С = ЕС ∩ АС₁.

е) Через точку С провести прямую СВ, параллельную С₁В₁, СВ ∩ АВ₁ = В. Треугольник АВС - искомый.

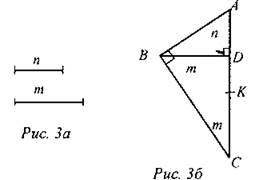
2. Построить отрезок если отрезки m и n известны.

В прямоугольном ∆АВС BD - высота, проведенная из вершины прямого угла, поэтому Если CK= m, to DK = m²: n - m.

Построение:

а) Построить ∆ABD, в котором ∠D = 90°, BD = m, AD = n.

б) Провести прямую ВС так, что ВС ⊥ AD = С.

в) На луче СА отложить отрезок СК, равный m.

г) DК - искомый отрезок.

Задача не имеет решения, если m < n

III этап. Самостоятельная работа

Цель деятельности

Задания для самостоятельной работы

Совершенствовать навыки решения задач методом подобия

(И) Вариант I

Постройте прямоугольный треугольник по острому углу и медиане, проведенной из вершины этого угла.

Вариант II

Постройте прямоугольный треугольник по острому углу и биссектрисе прямого угла

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою работу на уроке.

- Какой этап урока был наиболее сложным?

(И) Домашнее задание: решить № 629