СРЕДНЯЯ ЛИНИЯ ТРЕУГОЛЬНИКА - ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для доказательства теоремы о средней линии треугольника и свойства медиан треугольника; для применения этих свойств в процессе решения задач

Термины и понятия

Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия, средняя линия треугольника

Планируемые результаты

Предметные умения

Универсальные учебные действия

Владеют базовым понятийным аппаратом по основным разделам содержания

Познавательные: понимают и используют математические средства наглядности для иллюстрации, интерпретации, аргументации; устанавливают причинно-следственные связи, строят логическое рассуждение, делают умозаключения и выводы.

Регулятивные: принимают и сохраняют цели и задачи учебной деятельности.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют ясно, точно, грамотно излагать свои мысли в устной и письменной речи.

Личностные: проявляют познавательные интерес к изучению предмета

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной и групповой работы

I этап. Активизация знаний учащихся

Цель деятельности

Совместная деятельность

Выявить трудности, возникшие при решении задач в контрольной работе

(Ф/И)

1. Сообщить результаты выполненной работы.

2. Обсудить решения задач, с которыми не справились большинство учащихся.

3. Предложить выполнить работу над ошибками самостоятельно дома

II этап. Мотивация к деятельности

Цель деятельности

Постановка учебной задачи

Подготовить учащихся к введению понятия средняя линия треугольника

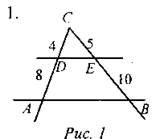
(Ф/И)

Повторить теоретический материал в процессе решения задач по готовым чертежам.

CD = 4, AD = 8, СЕ = 5, BE = 10.

Доказать: a) ∆CDE ~ ∆САВ;

б) AB || DE

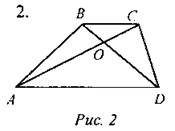
ABCD - трапеция.

Доказать: а) ВО : OD = СО : ОА;

б) DO : ВО = 2, если ВС = AD/2

III этап. Учебно-познавательная деятельность

Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятие средней линии трапеции и доказать теорему о средней линии трапеции

(Ф/И) 1. Определение средней линии треугольника.

Определение. Отрезок, соединяющий середины двух сторон треугольника, называется средней линией треугольника.

На доске и в тетрадях Picture из учебника на с. 145 и запись: “Если AM = МВ и CN = NB, то MN - средняя линия ∆АВС”.

(Г) 2. Творческое задание.

Работа осуществляется в группах с последующим обсуждением решения.

- Исследуйте, какими свойствами обладает средняя линия треугольника.

3. Оформление теоремы о средней линии треугольника с доказательством на доске и в тетрадях.

4. Решение задач № 564, 565 (устно, рисунки на доске выполнены заранее).

№ 564.

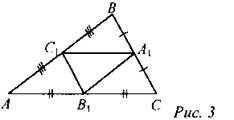
Дано: ∆АВС, АВ = 8 см, ВС = 5 см, АС = 7 см; А₁ є ВС, В₁є АС, С₁ є АВ; А₁, В₁, С₁ — середины сторон ∆АВС.

Найти Р_AB1C1.

Решение:

1) А₁В₁, B₁C₁, A₁C₁ - средние линии ∆АВС, значит,

2)

№ 565.

Дано: ABCD - прямоугольник, АС ∩ BD = О, ОН ⊥ AD, ОН = 2,5 см.

Найти: АВ.

Решение:

1) Рассмотрим ∆АОН и ∆ACD: ∠A - общий, ∠H = ∠D = 90°, следовательно, ∆АОН ~ ∆ACD, следовательно, Так как О - середина АС, то АО = 1/2АС, значит,

(Г) 5. Творческое задание. Задача № 1, с. 146 (учащиеся работают в группах по 3-4 человека).

Доказать, что медианы треугольника пересекаются в одной точке, которая делит каждую медиану в отношении 2:1, считая от вершины.

6. Решение задачи с целью закрепления свойства медиан треугольника (устно).

В треугольнике АВС медианы АА₁, ВВ₁ и СС₁, равные соответственно 6 см, 9 см и 12 см, пересекаются в точке О.

Найти: АО + ОВ + СО

IV этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач на применение знаний о подобных треугольниках

(Ф/И) Решить на доске и в тетради № 567 и 570

№ 567.

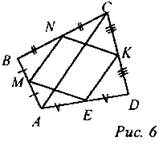
Дано: ABCD - четырехугольник, M, N, K, E -середины сторон.

Доказать: MNKE - параллелограмм.

Доказательство:

1) Рассмотрим ∆АВС и ∆MBN: ∠B - общий, (по условию), следовательно, ∆ABC ~ ∆MBN (по двум сторонам и углу между ними), следовательно, MN = 1/2AC и MN ⊥ АС.

2) Рассмотрим ∆АВС. КЕ - средняя линия ∆ADC(по определению), значит, КЕ = 1/2АО и КЕ || АС.

3) Вывод: MN = КЕ = 1/2АС.

КЕ || MN || АС => MNKE - параллелограмм по признаку, что и требовалось доказать.

№ 570.

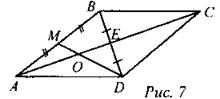
Дано: ABCD - параллелограмм, АС = 18 см, Mє AB, AM = MB, MD ∩ AC = О.

Найти: АО, ОС.

Решение:

1) Рассмотрим ∆ABD. DM, АЕ - медианы и АЕ ∩DM = О, по свойству медиан АО : ОЕ = 2 : 1.

2) Так как (свойство диагонали параллелограмма) АЕ = 9 см, тогда АО = 6 см, ОЕ = 3 см, отсюда ОС = ОЕ + ЕС = 3 + 9 = 12 см.

Ответ: 6 см, 12 см.

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Составьте синквейн к уроку.

- Оцените свою работу

(И) Домашнее задание: вопросы 8, 9, с. 159; № 565, 566, 571