КОНТРОЛЬНАЯ РАБОТА № 3 - ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для проверки знаний, умений и навыков учащихся по усвоению и применению изученного материала

Термины и понятия

Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности

Познавательные: проводят сравнение, сериацию и классификацию по заданным критериям.

Регулятивные: вносят необходимые коррективы в действие после его завершения на основе его учета характера сделанных ошибок; осуществляют самоанализ и самоконтроль.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.

Личностные: понимают важность и необходимость знаний для человека

Организация пространства

Формы работы

Индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Выполнение контрольной работы

Цель деятельности

Задания для контрольной работы

Проверить знания, умения и навыки по изученному материалу

(И)

Вариант I

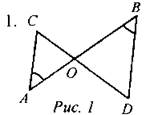
Дано: ∠A = ∠B, СО = 4, DO = 6, АО = 5.

Найти: а) ОВ\ б) АС : BD\ в) S_AOC : S_BOD.

2. В треугольнике АВС АВ = 4 см, ВС = 1 см, АС = 6 см, а в треугольнике MNK МК = 8 см, MN = 12 см, KN = 14 см. Найдите углы треугольника MNK, если ∠А = 80°,∠В = 60°.

3. Прямая пересекает стороны треугольника АВС в точках Ми К соответственно так, что МК || АС, ВM : AM = 1 : 4. Найдите периметр треугольника ВМК, если периметр треугольника АВС равен 25 см.

4*. В трапеции ABCD (AD и ВС - основания) диагонали пересекаются в точке О, AD = 12 см, ВС = 4 см. Найдите площадь треугольника ВОС, если площадь треугольника AOD равна 45 см².

Вариант II

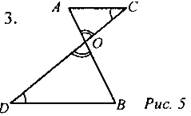
Дано: PE || NK, MP = 8, MN = 12, ME = 6.

Найти: а) МК; б) РЕ : NK; в) S_MEP : S_MKN.

2. В ∆АВС АВ = 12 см, ВС = 18 см, ∠B = 70°, а в ∆MNK MN = 6 см, NK = 9 см, ∠N = 70°. Найдите сторону АС и угол С треугольника АВС, если МК = 1 см, ∠K = 60°.

3. Отрезки АВ и CD пересекаются в точке О так, что ∠ACO = ∠BDO, АО : ОВ = 2 : 3. Найдите периметр треугольника АСО, если периметр треугольника BOD равен 21 см.

4*. В трапеции ABCD (AD и ВС - основания) диагонали пересекаются в точке О, S_AOD = 32 см², S_BOC = 8 см². Найдите меньшее основание трапеции, если большее из них равно 10 см.

Решение заданий контрольной работы

Вариант I

1. ∆АОС ~ ∆BOD по двум углам. АО : ВО = СО : DO => ОВ = 7,5. АС : BD = 2 : 3. S_AOC ∙ S_BOD = 4 : 9.

Ответ: а) 7,5; б) 2 : 3; в) 4 : 9.

2. AB : MK = 1 : 2, BC : KN = 1 : 2, AC : MN = 1 : 2. ∆ABC ~ ∆MKN. ∠M = ∠A = 80°, ∠K = ∠B = 60°. ∠N = 180° - (∠M + ∠K) = 40°.

Ответ: 80°, 60°, 40°.

а) ∆ВМК ~ ∆BAC по двум углам => ВМ : ВА = МК : АС = ВК : ВС = 1/5.

б) Р_ВMK : P_ABC = 1 : 5, значит, Р_ВMK = 5 см.

Ответ: 5 см.

a) ∆BOC ~ ∆DOA.

б) BO : DO = OC : OA = BC : DA = 4 : 12 = 1 : 3 = k.

в) S_BOC : S_DOC = k² = 1/9, значит, S_BOC = 5 см².

Ответ: 5 см².

Вариант II

1. ∆МРЕ ~ ∆MNK по двум углам. МР : MN = ME : МК => МК = 9. РЕ : NK = 2 : 3. S_MPE : S_MKN = 4 : 9.

Ответ: а) 9; б) 2 : 3; в) 4 : 9.

2. AB : MN = 2, BС : NK = 2, ∠B = ∠N => ∆ABC ~ ∆MNK АС : МК = 2 => АС = 14 см, ∠C = ∠K = 60°.

Ответ: АС = 14 см, ∠C = 60°.

а) ∆АСО ~ ∆BDO по двум углам => AС : BD = СО : DO = AO : ВО = 2 : 3.

б) P_ACO : P_ADO = 2 : 3 => P_ACO = 14 см.

Ответ: 14 см.

а) ∆ВОС ~ ∆DOA.

б) S_BOC : S_DOA = 8 : 32 = 1/4 = k², k = 0,5.

в) ВС : AD = k = 0,5, значит, ВС = 5 см.

Ответ: 5 см

II этап. Итоги урока

Деятельность учителя

Деятельность учащихся

(И) Домашнее задание: повторить § 2 главы VII и теорему Фалеса