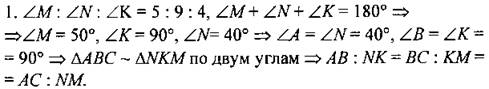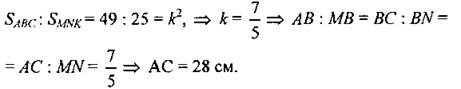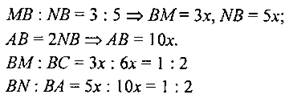РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ПРИЗНАКОВ ПОДОБИЯ ТРЕУГОЛЬНИКОВ - Урок 2 - ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для совершенствования навыков решения задач на применение признаков подобия треугольников для подготовки учащихся к контрольной работе

Термины и понятия

Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности

Познавательные: осуществляют поиск необходимой информации для выполнения учебных заданий с использованием учебной литературы.

Регулятивные: умеют адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, контролировать действие партнера, работать в группе, осуществлять самоанализ и самоконтроль.

Коммуникативные: вступают в речевое общение, участвуют в диалоге.

Личностные: проявляют познавательный интерес к изучению предмета

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Учебник.

• Задания для групповой и индивидуальной работы

I этап. Проверка домашнего задания

Цель деятельности

Совместная деятельность

Проверить уровень усвоения признаков подобия треугольников

(Ф/И)

1. Ответить на вопросы учащихся.

2. Проверить выполнение домашнего задания.

№ 562.

Дано: ∆АВС, АВ = а, СН ⊥ АВ, СН = h, MNKE - квадрат.

Найти: MN.

Решение:

Рассмотрим ∆АВС и ∆KNC. ∠B = ∠N (как соответственные при АВ || NK и секущей ВС), ∠C — общий, следовательно, ∆ABC ~ ∆KNC (по двум углам), следовательно,

Примем MN = NK = КЕ = ME = х, следовательно, CQ = h - х. Подставим значения в (*), получим: то есть

Ответ:

№ 563.

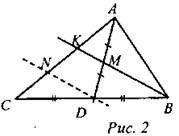
Дано: ∆ABC, AD - медиана, M є AD, BM ∩ AC = K.

Найти:

Решение:

а) Если M - середина AD (дополнительное построение ND || КВ):

1) Рассмотрим ∆АКМ и ∆AND; ∠A - общий, ∠K = ∠N (как соответственные при КВ || AD и секущей AN), следовательно, ∆АКМ ~ ∆AND (по двум углам), следовательно, (так как AM = MD по условию).

2) Рассмотрим ∆CND и ∆СКВ; ∠C - общий, ∠D = ∠B (как соответственные при ND || КВ и секущей DB), следовательно, ∆CND ~ ∆СКВ (по двум углам), следовательно, (так как CD = DB по условию).

3) следовательно, АК = NK = CN, а значит что и требовалось доказать.

б) Если рассуждая аналогично пункту (а), имеем:

1) ∆АКМ ~ ∆AND (по двум углам), следовательно,

2) ∆NCD ~ ∆СКВ (по двум углам), следовательно,

3) то есть АК : KN = 1 : 2; то есть CN = NK = 2. Значит, что и требовалось доказать

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Совершенствовать навыки решения задач на применение признаков подобия треугольников; подготовить учащихся к контрольной работе

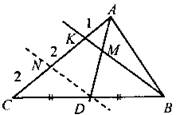
(Г) Класс делится на группы по 3—4 человека. Учитель при необходимости оказывает консультативную помощь.

Задачи:

1. В прямоугольном треугольнике ABC ∠A = 40°, ∠B = 90°, а в треугольнике MNK углы М, N, К относятся как 5:9:4.

АВ = 3 см, KN = 9 см.

Найти: а) ВС : КМ; б) S_ABC ∙ S_MNK; в) Р_ABC : Р_MNK.

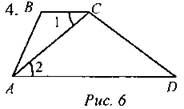
Дано: MN ll AC, S_ABC : S_BMN = 49 : 25, MN = 20 см.

Найти: АС.

3. В параллелограмме ABCD АЕ - биссектриса угла А. Стороны параллелограмма АВ и ВС относятся как 4 : 9. АЕ пересекает диагональ BD в точке К. Найти отношение ВК : KD.

4. В трапеции ABCD основания ВС и AD равны 2 см и 8 см, а диагональ АС равна 4 см. В каком отношении делит диагональ АС площадь трапеции?

5. Прямая MN пересекает стороны АВ и ВС треугольника АВС в точках Ми N соответственно так, что ВС = 2МВ, АВ = 2NB, МВ : NB = 3 : 5.

Найти: а) Р_ABC : Р_NBM, б) S_ABC : S_NBM, в) MN : АС

Краткое решение задач:

а) Так как АВ : NK = 3 : 9 = 1 : 3, то ВС : КМ = 1 : 3.

Ответ: а) 1 : 3; б) 1 : 9; в) 1 : 3.

2. ∆АВС ~ ∆BMN по двум углам (∠B - общий, ∠BAC =∠BMN).

Ответ: 28 см.

Биссектриса ∠A параллелограмма ABCD отсекает от него равнобедренный треугольник АВЕ, следовательно, АВ =BE. Так как АВ : ВС = 4 : 9, то BE : ВС = 4 : 9. BE : AD = 4 : 9 (ВС = AD, как противолежащие стороны параллелограмма).

∆AKD ~ ∆EKB по двум углам (∠BKE = ∠AKD, ∠BEK =∠KAD), тогда ВК : KD = BE : AD = 4 : 9.

Ответ: 4 : 9.

∆АВС ~ ∆DCA по двум пропорциональным сторонам и углу между ними (ВС : АС = АС : AD = 1 : 2; ∠1 = ∠2),отсюда

Ответ: 1 : 4.

∠MBN = ∠CBA, таким образом, ∆ABC ~ ∆NBM.

Отвeт: a) 1 : 2: 6) 4 : 1: в) 1 : 2

III этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою работу и работу группы.

- Какая задача оказалась для вас трудной и почему?

(И) Домашнее задание: решить задачи.

1. Высота CD прямоугольного треугольника АВС делит гипотенузу АВ на части AD = 16 см иBD = 9 см. Докажите, что ∆ACD ~ ∆CBD, и найдите высоту CD.

2. Точки М и N лежат на сторонах АС и ВС треугольника АВС соответственно, АС = 16 см, ВС = 12 см, СМ = 12 см, CN = 9 см. Докажите, что MN ll BC