Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ПЕРВЫЙ ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ. РЕШЕНИЕ ЗАДАЧ - ПОДОБНЫЕ ТРЕУГОЛЬНИКИ
|
Цель деятельности учителя |
Создать условия для формирования у учащихся навыков решения задач на применение первого признака подобия треугольников |
||||
|
Термины и понятия |
Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия |
||||
|
Планируемые результаты |
|||||
|
Предметные умения |
Универсальные учебные действия |
||||
|
Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности |
Познавательные: осуществляют логические действия; формулируют ответы на вопросы. Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, контролировать процесс и результат учебной математической деятельности. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве; умеют работать в группе. Личностные: проявляют познавательный интерес к изучению предмета |
||||
|
Организация пространства |
|||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
||||
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной, индивидуальной работы |
||||
|
I этап. Актуализация опорных знаний |
|||||
|
Цель деятельности |
Совместная деятельность |
||||
|
Проверить правильность выполнения домашней работы |
(Ф) 1. Проверка домашнего задания. 2. Теоретический опрос: - Сформулируйте первый признак подобия треугольников. - Чему равно отношение периметров подобных треугольников? - Какие треугольники называются подобными? - Сформулируйте теорему об отношении площадей подобных треугольников. 3. Найти пары подобных треугольников (устно):
|
||||
|
II этап. Решение задач по готовым чертежам |
|||||
|
Цель деятельности |
Задания для самостоятельной работы |
||||
|
На простых задачах проверить уровень усвоения первого признака подобия треугольников |
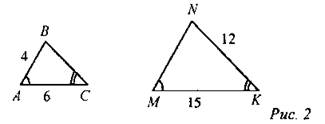
(И) Учащиеся самостоятельно решают данные задачи, затем решение каждой задачи выносится на доску. Проводится обсуждение решений и осуществляется самооценка. 1. Найти: ВС, MN.
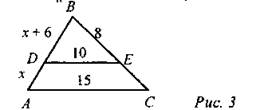
Ответ: ВС = 3,2, MN = 22,4. 2. Дано: DE || АС. Найти: АВ, ВС.
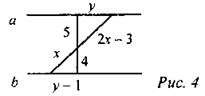
Ответ: AB = 18, ВС = 12. 3. Дано: а || b. Найти: х, у.
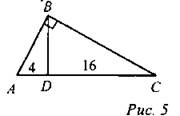
Ответ: х = 4, у = 5. 4. Найти: BD.
Ответ: BD = 8. 5. Найти: СО, ВО.
Ответ: СО = 4, ВО = 12 6. Найти: ВС.
Ответ: ВС = 15 |
||||
|
III этап. Решение задач |
|||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
|||
|
Отработать применение первого признака подобия при решении задач |
(Ф) 1. Решите № 556. 2. Решите № 557 (а). (И/П) 3. Самостоятельно решите № 557 (б), 552 (в) в парах. (Затем проверка на доске.) 4. Решите задачу: Диагонали трапеции ABCD с основаниями AD и ВС пересекаются в точке О. Периметры треугольников ВОС и AOD относятся как 2 : 3, АС = 20. Найдите длины отрезков АО и ОС |
№ 557 (а). Краткое решение:
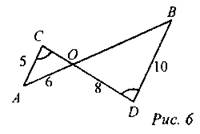
Ответ: АС = 17,5 см. № 557 (б). Краткое решение:
Ответ: BD = 5 см, DE = 6 см. № 552 (в). Краткое решение (рис. 461): Пусть АО = х см, тогда ОС = АС - АО = 15 - x (см).
120x = 1440; x = 12 (см), то есть АО = 12 см. Ответ: АО = 12 см. Решение:
∆ВОС ~ ∆DOА по двум углам (∠CBO = ∠ADO, ∠BCO =∠DAO, как накрест лежащие при параллельных прямыхAD и ВС и секущих АС и BD), тогда Ответ: АО = 12, ОС = 8 |
|||
|
IV этап. Итоги урока. Рефлексия |
|||||
|
Деятельность учителя |
Деятельность учащихся |
||||
|
(Ф/И) - Оцените свою работу на уроке. - Какие трудности возникли у вас при решении задач? - Кто может с полной уверенностью сказать, что понял, как применять первый признак подобия треугольников при решении задач? |
(И) Домашнее задание: повторить п. 59; решить задачи № 552 (а, б), 557(b), 558,556 |
||||


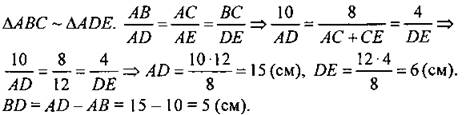
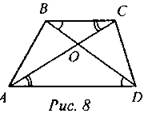
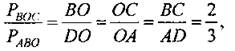 то есть ОС : ОА = 2 : 3, ОА = 1,5ОС. Так как АС = 20, то АС = ОА + ОС = 1,5OС + ОС = 20, откуда ОС = 8, тогда AО = 12.
то есть ОС : ОА = 2 : 3, ОА = 1,5ОС. Так как АС = 20, то АС = ОА + ОС = 1,5OС + ОС = 20, откуда ОС = 8, тогда AО = 12.