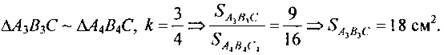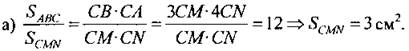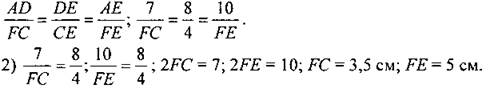ПЕРВЫЙ ПРИЗНАК ПОДОБИЯ ТРЕУГОЛЬНИКОВ - ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для выведения доказательства первого признака подобия треугольников и формирования у учащихся навыков применения этого признака при решении задач

Термины и понятия

Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности

Познавательные: осуществляют логические действия; формулируют ответы на вопросы.

Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения, контролировать процесс и результат учебной математической деятельности.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве, умеют работать в группе.

Личностные: проявляют познавательный интерес к изучению предмета

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Активизация знаний учащихся

Цель деятельности

Совместная деятельность

Проверить правильность выполнения домашней работы

(Ф) Проверка домашнего задания: № 544, 543, 546, 549 (дополнительную задачу проверить индивидуально)

II этап. Мотивация к деятельности

Цель деятельности

Постановка учебной задачи

Подготовить учащихся к восприятию новой темы

(Ф/И) Решение задач с целью подготовки учащихся к восприятию нового материала. (Самостоятельное решение с последующим обсуждением.) Обсуждение решений можно организовать таким образом: один из учащихся выходит к доске и предлагает свое решение, остальные предлагают свое или соглашаются с предложенным решением.

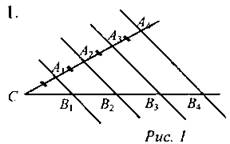
Решение:

По теореме Фалеса СВ₁ = В₁В₂ = В₂В₃ = В₃В₄ = 3 см, следовательно, В₂В₄ = 6 см.

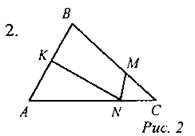
Ответ: В₁В₂ = 3 см, В₂В₄ = 6 см, S_A3B3C = 18 см².

Дано: S_ABC = 36 см², AN : NC = 3 : 1, ВМ : МС = 2 : 1, АК = КВ.

Найти: a) S_CMN; б) S_AKN; в) S_BKNM.

Решение:

Ответ: a) S_CMN = 3 см²; б) S_AKN — 13,5 см²; в) S_BKNM = 19,5 см²

III этап. Изучение новой темы

Цель деятельности

Совместная деятел ьность

Доказать первый признак подобия треугольников

(Ф/И) 1. Сформулировать первый признак подобия треугольников.

2. Доказать первый признак подобия треугольников и записать план доказательства на доске и в тетрадях

IV этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Научить применять доказанную теорему при решении задач

(Ф/И) Решить задачи № 550, 551, 553, 561 (устно)

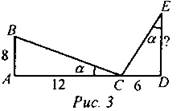
№ 550.

а) Рассмотрим ∆AВС и ∆CDE. ∠C = ∠E = α (по условию), ∠A = ∠D = 90° (по условию), следовательно, ∆ABC ~ ∆DCE (по двум углам), следовательно,

б)

1) Рассмотрим ∆АВС и ∆DEC. ∠A = ∠D = 90° (по условию), ∠C - общий, следовательно,∆ABC ~ ∆DEC (по двум углам), следовательно, (по теореме Пифагора).

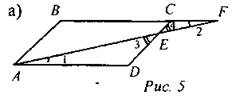
№ 551.

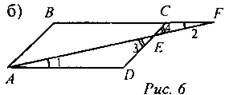
Дано: ABCD - параллелограмм.

Е є CD, АЕ ∩ ВС = F, DE = 8 см, ЕС = 4 см, ВС = 7 см, АЕ = 10 см.

Найти: EF, FC.

Решение:

1) Рассмотрим ∆AED и ∆FCE. ∠1 = ∠2 (как накрест лежащие при AD ll ВС и секущей AF),∠3 = ∠4 (как вертикальные), следовательно

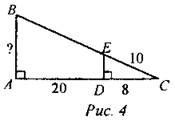
Дано: ABCD - параллелограмм.

АВ = 8 см, AD = 5 см, CF = 2 см.

Найти: DE, ЕС.

Решение:

Из ∆AED ~ ∆FED следует, что

Так как DE + ЕС = CD = 8 см, то

№ 553.

а) да; б) да; в) да.

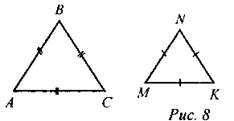
Так как треугольники равнобедренные и имеют по одному равному углу, то, используя свойство углов равнобедренного треугольника и теорему о сумме углов треугольника, можно найти остальные углы.

Следовательно, ∆ABC ~ ∆A₁B₁C₁ по двум углам.

№ 561.

Дано: ∆АВС и ∆MNK

АВ = ВС = АС

MN = NK = МК

Доказать: ∆ABC ~ ∆MNK

Доказательство:

1) ∆ABC - равносторонний, значит, ∠А = ∠В = ∠С = 60°

∆MNK - равносторонний, значит, ∠М = ∠N = ∠К = 60°.

2) Так как ∠M = ∠N = ∠К = ∠А = ∠В = ∠С = 60°, то ∆ABC ~ ∆MNK по двум углам, что и требовалось доказать

V этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Для того чтобы записать пропорциональность сторон подобных треугольников, что необходимо?

- Сформулируйте первый признак подобия треугольников.

- Составьте синквейн к уроку

(И) Домашнее задание: выучить признак подобия треугольников; решить № 555.

Дополнительная задача:

На продолжении сторон DC (за точку С) и ВА (за точку А) параллелограмма ABCD взяты соответственно точки К и Е. КЕ пересекает сторону ВС в точке М, а сторону AD - в точке F.Докажите, что АЕ ∙ МС = КС ∙ AF