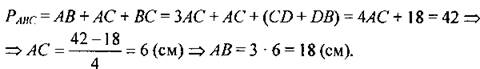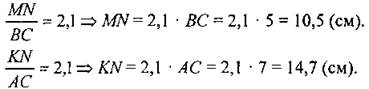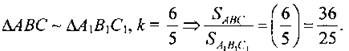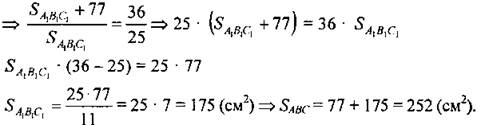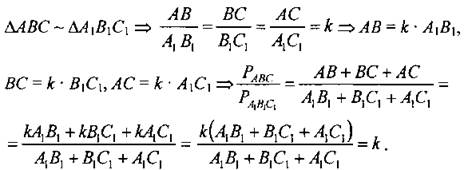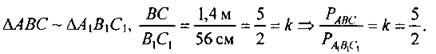ОТНОШЕНИЕ ПЛОЩАДЕЙ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ - ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для закрепления понятий пропорциональных отрезков и подобных треугольников; для совершенствования навыков решения задач на применение свойства биссектрисы треугольника и определения подобных треугольников; для рассмотрения теоремы об отношении площадей подобных треугольников и ее применения в процессе решения задач

Термины и понятия

Пропорциональные отрезки, отношение, пропорции, сходственные стороны, коэффициент подобия

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности

Познавательные: осуществляют логические действия; формулируют ответы на вопросы.

Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве, умеют работать в группе.

Личностные: проявляют способность к эмоциональному восприятию математатических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И); групповая (Г)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной, фронтальной работы

I этап. Активизация знаний учащихся

Цель деятельности

Деятельность учителя

Деятельность учащихся

Выявить трудности, возникшие при выполнении домашнего задания; подготовить учащихся к восприятию новой темы

(Ф/И)

1. К доске вызвать троих учащихся: один из них готовит доказательство теоремы, двое оформляют на доске задачи № 538 и № 542.

2. В это время остальные учащиеся отвечают на теоретические вопросы, а затем решают задачи на готовых чертежах.

1) Что называется отношением двух отрезков?

2) В каком случае говорят, что отрезки АВ и CD пропорциональны отрезкам А₁В₁ и С₁D₁?

3) Дайте определение подобных треугольников.

Задачи:

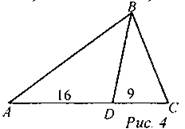
3) Двое учащихся работают по индивидуальным карточкам.

1-й уровень (карточка 1).

1. Треугольники KPF и ЕМТ подобны, причем КР : ME = PF : МТ = KF : ЕТ, ∠F = 30°, ∠E = 49°. Найдите остальные углы этих треугольников.

2. Биссектриса BD делит сторону АС треугольника АВС на отрезки AD и CD, равные соответственно 7 см и 10,5 см. Найдите периметр треугольника АВС, если известно, что АВ = 9 см.

2-й уровень (карточка 2).

1. Дано: ∆BDC ~ ∆ABC, AD = 16 см, DC = 9 см. ∠ABC и ∠BDA - тупые.

Найти: ВС.

2. Периметр треугольника равен 70 см, две его стороны равны 24 и 32 см. Найдите отрезки, на которые биссектриса треугольника делит его третью сторону

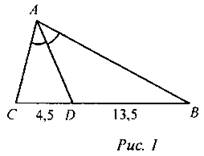
№ 538.

AD - биссектриса ∆ABC =>

Ответ: AС = 6 см, АВ = 18 см.

№ 542.

Ответ: КМ = 8,4 см, MN = 10,5 см, KN = 14,7 см

II этап. Изучение новой темы

Цель деятельности

Совместная деятельность

Доказать теорему об отношении площадей подобных треугольников

(Г)

1. Распределить учащихся по творческим группам и предложить обсудить в группах задачу: “Треугольники АВС и А₁В₁С₁ подобны с коэффициентом подобия k. Найти отношение их площадей”.

2. Заслушать варианты решений, выбрать из предложенных наиболее удачный и решение записать в тетрадях и на доске

III этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

Научиться применять доказанную теорему

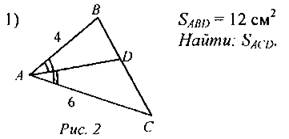
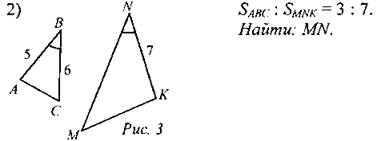
(Ф/И)

1. Решить письменно задачу № 545 на доске и в тетрадях (записать краткое решение). Один из учащихся самостоятельно решает задачу на доске, остальные - в тетрадях. После завершения работы проверяется правильность решения.

(Г) 2. Решить задачи № 547, 548 (обсудить принцип решения задач, варианты решений заслушать всем классом)

№ 545.

S_ABC на 77 см² больше

Ответ: 175 см² и 252 см².

№ 547.

Краткое решение:

№ 548.

Краткое решение:

Ответ: 5 : 2

Самостоятельная работа

Цель деятельности

Задания для самостоятельной работы

Закрепить полученные знания

(И) Учащиеся выполняют самостоятельную работу на листочках и сдают на проверку учителю (если время на уроке осталось, можно выполнить самопроверку) (см. Ресурсный материал)

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою работу на уроке.

- На каком этапе урока у вас возникли наибольшие затруднения?

(И) Домашнее задание: п. 60, вопрос 4; повторить п. 52; решить задачи № 544, 543, 546, 549; решить задачу (по желанию):

В трапеции ABCD (AD ll ВС) АС - биссектриса ∠A делит трапецию на два подобных треугольника АВС и ACD, АВ = 9 см, CD = 12 см. Найдите периметр трапеции