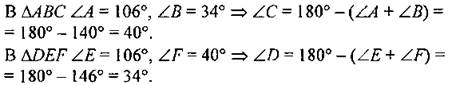ПРОПОРЦИОНАЛЬНЫЕ ОТРЕЗКИ. ОПРЕДЕЛЕНИЕ ПОДОБНЫХ ТРЕУГОЛЬНИКОВ - ПОДОБНЫЕ ТРЕУГОЛЬНИКИ

Цель деятельности учителя

Создать условия для определения пропорциональных отрезков, рассмотрения свойства биссектрисы треугольника и применения этого свойства при решении задач

Термины и понятия

Пропорциональные отрезки, биссектриса угла, отношение, пропорции, сходственные стороны, коэффициент подобия

Планируемые результаты

Предметные умения

Универсальные учебные действия

У меют демонстрировать знание основных понятий, применять полученные знания для решения основных и качественных задач, контролировать процесс и результат учебной математической деятельности

Познавательные: осуществляют логические действия; формулируют ответы на вопросы.

Регулятивные: умеют самостоятельно ставить цели, выбирать и создавать алгоритмы для решения математических проблем, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.

Личностные: проявляют способность к эмоциональному восприятию математатических объектов, задач, решений, рассуждений

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник

I этап. Анализ контрольной работы

Цель деятельности

Совместная деятельность

Выявить трудности, возникшие при решении задач в контрольной работе

(Ф/И)

1. Сообщение итогов контрольной работы.

2. Анализ ошибок, допущенных учащимися в ходе работы.

3. Решение на доске задач, вызвавших затруднения у учащихся

II этап. Мотивация к деятельности

Цель деятельности

Постановка учебной задачи

Подготовить учащихся к введению понятия пропорциональных отрезков

(Ф)

- Что называют отношением двух чисел? Что показывает отношение?

- Отношение АВ к CD равно 2:7.0 чем это говорит? Найдите отношение CD к АВ.

- В ∆АВС АВ : ВС : АС = 2 : 4 : 3, Р_АВC = 45 дм. Найдите стороны треугольника АВС.

- Что называют пропорцией? Верны ли пропорции 1,5 : 1,8 = 25 : 30; 18 : 3 = 5 : 30?

- В пропорции а : b = с : d укажите крайние и средние члены. Сформулируйте основное свойство пропорции.

- Переставив средние или крайние члены пропорции, составьте три верные пропорции: а) 12 : 0,2 = 30 : 0,5; б) АВ : MN = CD : КР.

- Найдите неизвестный член пропорции, a) 1x : 4,2 = 12,3 : 6; б) х : АВ = MN : КР

III этап. Изучение нового материала

Цель деятельности

Совместная деятельность

Ввести понятие пропорциональных отрезков

(Ф)

1. Ввести понятие отношения отрезков.

Определение. Отношением отрезков АВ и CD называется отношение их длин, то есть АВ : CD.

2. Ввести понятие пропорциональных отрезков.

Определение. Отрезки АВ и CD пропорциональны отрезкам А₁В₁ и С₁D₁, если АВ : А₁В₁ = CD : C₁D₁.

Например:

Если АВ = 5 см, CD = 7 см, А₁В₁ = 7,5 см, C₁D₁ = 10,5 см, то АВ : А₁В₁ = CD : C₁D₁, то есть отрезки АВ и CD пропорциональны отрезкам А₁В₁ и C₁D₁.

3. Ввести понятие подобных фигур (два круга, два квадрата, два мяча разных размеров, изображения на кинопленке и на экране, на фотопленке и на фотографии и т. д.).

4. Ввести понятие подобных треугольников:

∆АВС ~ ∆А₁В₁С₁, если ∠A = ∠A₁, ∠B = ∠B₁, ∠C = ∠C₁ и где k - коэффициент подобия.

Стороны АВ и А₁В₁, ВС и В₁С₁, АС и A₁C₁ называют сходственными.

Определение. Два треугольника называются подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

5. Решить устно № 533, 534 (а, б).

6. Разобрать решение задачи № 535 (свойство биссектрисы треугольника)

IV этап. Закрепление изученного материала

Цель деятельности

Деятельность учителя

Деятельность учащихся

При решении простых задач отработать понятия пропорциональных отрезков и сходственных сторон

(Ф/И) 1. Один из учащихся решает задачу № 536 (б) на доске, остальные в тетрадях.

2. Решить самостоятельно № 541. Затем один из учеников выходит к доске, показывает решение, остальные сверяют, задают вопросы, оценивают себя

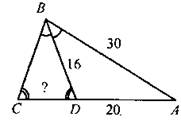
№ 536 (б).

Решение:

Так как ∠C = ∠BDC, то ∆BDC - равнобедренный с основанием CD, следовательно, ВС = BD = 16.

Так как BD - биссектриса ∆АВС, то

Ответ:

№ 541.

Решение:

По определению подобных треугольников, два треугольника называют подобными, если их углы соответственно равны и стороны одного треугольника пропорциональны сходственным сторонам другого.

Ответ: ∆АВС ~ ∆DEF

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Какие новые понятия узнали?

- Какие отрезки называются пропорциональными?

- Какие стороны треугольника называются сходственными?

- Оцените по пятибалльной шкале, насколько вы поняли материал урока

(И) Домашнее задание: п. 58, 59, вопросы 1, 2, 3; решить задачи № 536 (а), 538, 542