РЕШЕНИЕ ЗАДАЧ НА ПРИМЕНЕНИЕ ТЕОРЕМЫ ПИФАГОРА - ПЛОЩАДЬ

Цель деятельности учителя

Создать условия для совершенствования навыков решения задач на применение теоремы Пифагора и теоремы, обратной теореме Пифагора

Термины и понятия

Прямоугольный треугольник, катеты, гипотенуза

Планируемые результаты

Предметные умения

Универсальные учебные действия

Умеют применять изученные понятия, методы для решения задач

Познавательные: осуществляют логические действия; формулируют ответы на вопросы.

Регулятивные: умеют самостоятельно планировать альтернативные пути достижения целей, осознанно выбирать наиболее эффективные способы решения учебных задач, адекватно оценивать правильность или ошибочность выполнения учебной задачи, ее объективную трудность и собственные возможности ее решения.

Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве.

Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики.

Организация пространства

Формы работы

Фронтальная (Ф); индивидуальная (И)

Образовательные

ресурсы

• Учебник.

• Задания для индивидуальной работы

I этап. Актуализация опорных знаний

Цель деятельности

Задания для самостоятельной работы

Проверить уровень сформированности знаний по теме

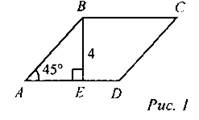
(Ф) 1. Теоретический опрос.

- Сформулировать теорему Пифагора.

- Сформулировать теорему, обратную теореме Пифагора.

(И) 2. Самостоятельное решение задач по готовым чертежам.

Решение с последующей проверкой и обсуждением (при необходимости) (количество предложенных задач можно изменить).

1. ABCD - параллелограмм.

Найти: CD.

2. DE || АС. Найти: АС.

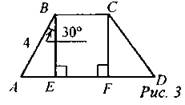
3. ABCD - трапеция. Найти: CF.

4. Найти: BD.

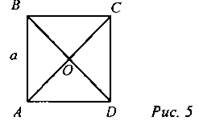
5. ABCD - квадрат. Найти: АО.

6. Найти: DC; АС; АВ.

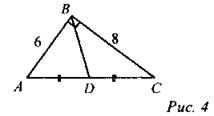
7. Найти: BD.

8. ABCD - параллелограмм. Найти: AD.

Ответы:

II этап. Решение задач

Цель деятельности

Деятельность учителя

Деятельность учащихся

Рассмотреть способы и методы решения задач повышенной сложности

(Ф) 1. Решить № 517, 496, 497, 489 на доске и в тетрадях

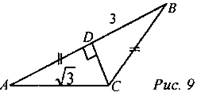
№ 496.

Дано: ∆АВС

CD ⊥ AB, AD = BC, AB = 3, CD = √3

Найти: АС.

Решение:

1) Примем ВС = AD = х, следовательно, в ∆DBC: ВС² = DC² + DB².

х² = (√3)² + (3 - x)²; х² = 3 + 9 – 6x + x²; 6x = 12; x = 2; BС = AD = 2 см.

2) В ∆АОС: АС² = АD² + ОС²; АС² = 4 + 3 = 7; АС = √7.

Ответ: √7.

№ 517.

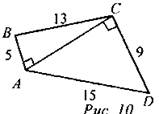
Дано: ABCD - четырехугольник

АВ = 5 см, ВС = 13 см, CD = 9 см, DA = 15 см, АС = 12 см.

Найти: S_ABCD.

Решение:

АВ² = 25, ВС² = 169, следовательно, 169 - 25 = 144 = AС²

CD² = 81, AD² = 225, следовательно, 225 - 81 = 144 = АС², значит ∆АВС и ∆АСD - прямоугольные с общей стороной АС = 12 см.

Ответ: 98 см².

№ 497.

Дано: ABCD - параллелограмм,

ВО ⊥ AD, Р_ABCD = 50 см, AD - AB = 1 см.

Найти: BD.

Решение:

1) Примем АВ = х см, следовательно, AD = (x + 1) см.

Так как P_ABCD = 2(АВ + AD), то 50 = 2 ∙ (х + х + 1); 25 = 2х + 1; 2х = 24; x = 12.

АВ = 12, AD = 13.

2) В ∆ABD: BD² = АВ²- AD²; BD² = 13² - 12²; BD² = 25, следовательно, BD = 5.

Ответ: 5 см.

№ 489.

Дано: ABC - равносторонний, АВ = а.

Доказать:

Доказательство:

1) Рассмотрим ∆ABB₁:

2)

а) если а = 5, то

б) если а = 1,2, то S_ABC = 0,36√3;

в) если а = 2√2, то S_ABC = 2√3

III этап. Самостоятельная работа

Цель деятельности

Задания для самостоятельной работы

Закрепить полученные знания

(И) При наличии времени можно предложить проверочную работу, которая сдается учителю.

Вариант I

В прямоугольной трапеции основания равны 22 см и 6 см, большая боковая сторона - 20 см. Найдите площадь трапеции.

Вариант II

В прямоугольной трапеции боковые стороны равны 7 см и 25 см, а меньшее основание равно 2 см. Найдите площадь трапеции.

Вариант III (для более подготовленных учащихся)

Диагональ АС прямоугольной трапеции ABCD перпендикулярна боковой стороне CD и составляет угол 60° с основанием AD. Найдите площадь трапеции, если AD = 24 см

IV этап. Итоги урока. Рефлексия

Деятельность учителя

Деятельность учащихся

(Ф/И)

- Оцените свою работу на уроке.

- Какой этап урока вам показался наиболее сложным? Почему?

(И) Домашнее задание: № 490,491; рассмотреть самостоятельно решение № 524 (вывод формулы Герона) (по желанию)