Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ТЕОРЕМА, ОБРАТНАЯ ТЕОРЕМЕ ПИФАГОРА - ПЛОЩАДЬ
|
Цель деятельности учителя |
Создать условия для выведения доказательства теоремы, обратной теореме Пифагора, и ее применения при решении задач' |
|||
|
Термины и понятия |
Прямоугольный треугольник, катеты, гипотенуза |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации в окружающей жизни. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соответствующее современному уровню развития науки и общественной практики |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Учебник. • Исторические сведения о применении теоремы Пифагора |
|||
|
I этап. Актуализация опорных знаний |
||||
|
Проверка домашнего задания |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Проверить, какие сообщения подготовили учащиеся |
(И) Учащиеся выступают со своими сообщениями или презентациями. (Ф) Учитель рассказывает о применении теоремы Пифагора (см. Ресурсный материал) |
|||
|
II этап. Мотивация к деятельности |
||||
|
Цель деятельности |
Постановка учебной задачи |
|||
|
Подвести учащихся к теореме, обратной теореме Пифагора |
(Ф) Сформулировать утверждения, обратные данным, и выяснить, верны ли они: • Сумма смежных углов равна 180°. • Диагонали ромба взаимно перпендикулярны. • Вертикальные углы равны. • В параллелограмме противолежащие стороны равны. • В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов. (В последнем случае учащиеся смогут сформулировать утверждение, обратное данному, а провести доказательство его справедливости может помочь учитель.) |
|||
|
III этап. Изучение нового материала |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Доказать теорему, обратную теореме Пифагора |
(Ф) 1. Учитель доказывает данную теорему. 2. Прямоугольные треугольники, длины сторон которых выражаются целыми числами, называются пифагоровыми треугольниками. Например, треугольник со сторонами 26, 24 и 10. - Приведите примеры пифагоровых треугольников. (10, 8 и 6; 13, 12 и 5; 5, 4 и 3; 15, 12 и 9 и другие.) 3. Являются ли пифагоровыми треугольники: а) с гипотенузой 25 и катетом 15; б) с катетами 5 и 4? 4. Треугольник со сторонами 3, 4, 5 был известен еще древним египтянам. Египтяне использовали его для построения прямых углов. Делали они это так: на веревке делали метки, делящие ее на 12 равных частей, связывали концы веревки и растягивали на земле с помощью кольев в виде треугольника со сторонами 3, 4 и 5. Угол, лежащий против стороны, равной 5, оказывался прямым. Этот треугольник получил название египетского треугольника и по сей день именно так его и называют |
|||
|
IV этап. Закрепление изученного материала |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
Закрепить изученные теоремы при решении простейших задач |
(Ф/И) 1. Решить № 498 (а, б, в) (устно). 2. Решить задачу № 499 (а). Один из учащихся по указанию учителя выходит к доске, остальные работают в тетрадях. 3. Решить самостоятельно задачи: а) Определите углы треугольника со сторонами 1,1, √2. (45°, 45°, 90°) б) В треугольнике АВС АВ = √2 , ВС = 2. На стороне АС отмечена точка М так, что АМ = 1, ВМ = 1. Найдите АС. (1 + √3.) в) В треугольнике МРК РК = 2. На стороне МК отмечена точка А так, что МА = АР = √3, АК = 1. Найдите ∠МРК. (75°.) |
№ 499 (а). 252 = 242 + 72, значит, треугольник прямоугольный и его площадь равна половине произведения его катетов, то есть S = 24 ∙ 7 : 2 = 84 см2. Меньшая высота проведена к большей стороне, а в прямоугольном треугольнике большей стороной является гипотенуза, значит, S = hc ∙ с : 2, где с -гипотенуза, hc - высота, проведенная к гипотенузе, тогда hc = 2S/c = 6,72 (см). Ответ: 6,72 см |
||
|
IV этап. Итоги у |
юка. Рефлексия |
|||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(И/Ф) Учащиеся продолжают фразы: • Теперь я узнал, что... • Теперь я могу... • Раньше я не понимал, как... • Раньше я не знал, что... • Теперь я знаю, что |
(И) Домашнее задание: п. 56; вопросы 9, 10; решить задачи № 498 (г, д, е), № 499 (б), 488 |
|||
Ресурсный материал
Применение теоремы Пифагора
В архитектуре.
В зданиях готического и романского стиля верхние части окон расчленяются каменными ребрами, которые не только играют роль орнамента, но и способствуют прочности окон.
Способ построения окна в готическом стиле очень прост. Легко найти центры шести дуг окружностей, радиусы которых равны ширине окна (b) для наружных дуг и половине ширины для внутренних дуг. Остается еще полная окружность, касающаяся четырех дуг. Так как она заключена между двумя концентрическими окружностями, то ее диаметр равен расстоянию между этими окружностями, то есть b/2 и, следовательно, радиус равен b/4. Тогда становится ясным и положение ее центра. В рассмотренном примере радиусы находились без всяких затруднений. В других аналогичных примерах могут потребоваться вычисления. Покажем, как применяется в таких задачах теорема Пифагора.
В романской архитектуре часто встречается мотив, представленный на рисунке. Если b по-прежнему обозначает ширину окна, то радиусы полуокружностей будут равны R = b/2 и r = b/4. Радиус р внутренней окружности можно вычислить из прямоугольного треугольника, катет которого изображен на рисунке пунктиром. Гипотенуза этого треугольника, проходящая через точку касания окружностей, равна b/4 + р, один катет равен b/4, а другой b/2 - р. По теореме Пифагора имеем: 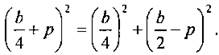 Решив данное уравнение, легко найти радиус внутренней окружности р = b/6.
Решив данное уравнение, легко найти радиус внутренней окружности р = b/6.
В строительстве.
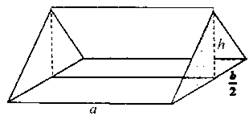
Возможно, кто-то сочтет приложения теоремы Пифагора сугубо теоретическими. Но это не так. Если, например, рассматривать треугольную призму как крышу башни, то в первом вопросе речь идет о том, какой длины нужно сделать боковые ребра, чтобы при данной площади чердака была выдержана предписанная высота крыши. Заметим, что расчет площади кровли можно сильно упростить, если воспользоваться одним очень простым правилом, справедливым во всех случаях, когда все скаты крыши, сколько бы их ни было, имеют одинаковый уклон. Оно гласит: “Чтобы найти площадь поверхности двускатной крыши, все скаты которой имеют равный уклон, нужно умножить площадь чердака Sч на длину стропила и разделить на половину ширины дома”.
При строительстве любого сооружения рассчитывают расстояния, центры тяжести, размещение опор, балок и т. д. В целом значение теоремы, кроме вышесказанного, в том, что она применяется практически во всех современных технологиях, а также открывает простор для создания и придумывания новых.
В физике.
Молниеотвод, громоотвод - устройство для защиты зданий, промышленных, транспортных, коммунальных, сельскохозяйственных и других сооружений от ударов молнии. Известно, что молниеотвод защищает от молнии все предметы, расстояние до которых от его основания не превышает его удвоенной высоты. Необходимо определить оптимальное положение молниеотвода на двускатной крыше, обеспечивающее наименьшую его доступную высоту.
По теореме Пифагора, h2 > а2 + b2, значит, ![]()
В астрономии.
В конце XIX века высказывались разные предположения о существовании обитателей Марса, подобных человеку. Это явилось следствием открытий итальянского астронома Скиапарелли (открыл на Марсе каналы, которые долгое время считались искусственными). Естественно, что вопрос о том, можно ли с помощью световых сигналов объясняться с этими гипотетическими существами, вызвал оживленную дискуссию. Парижской академией наук была даже установлена премия в 100 000 франков тому, кто первый установит связь с каким-нибудь обитателем другого небесного тела; эта премия все еще ждет счастливца. В шутку, хотя и не совсем безосновательно, было решено передать обитателям Марса световой сигнал в виде теоремы Пифагора. Неизвестно, как это сделать; но для всех очевидно, что математический факт, выражаемый теоремой Пифагора, имеет место всюду, и поэтому похожие на нас обитатели другого мира должны понять такой сигнал.
В литературе.
Многие, услышав имя Пифагор, вспоминают известную теорему, но мало кто знает, что этот знаменитый грек имел отношение не только к математике, но и к литературе.
Великий математик был еще и великим философом своего времени. Вот некоторые его высказывания:
• Делая великое, не обещай великого.
• Как ни коротки слова “да” и “нет”, всё же они требуют самого серьезного размышления.
• Не делай ничего постыдного ни в присутствии других, ни втайне.
• Первым твоим законом должно быть уважение к самому себе.
• Не закрывай глаз, когда хочешь спать, не разобравши всех своих поступков за прошедший день.
• По торной дороге не ходи.
Теорема Пифагора издавна широко применялась в разных областях науки, техники и практической жизни. О ней писали в своих произведениях римский архитектор и инженер Витрувий, греческий писатель-моралист Плутарх, греческий ученый III в. Диоген Лаэрций, математик V в. Прокл и многие другие.
Легенда о том, что в честь своего открытия Пифагор принес в жертву быка или, как рассказывают другие, сто быков, послужила поводом для юмора в творчестве писателей и поэтов. Так, например, немецкий писатель-романист А. Шамиссо, который в начале XIX в. участвовал в кругосветном путешествии на русском корабле “Рюрик”, написал следующие стихи:
Пребудет вечной истина, как скоро
Ее познает слабый человек!
И ныне теорема Пифагора
Верна, как и в его далекий век.
Обильно было жертвоприношенье
Богам от Пифагора. Сто быков
Он отдал на закланье и сожженье
За света луч, пришедший с облаков.
Поэтому всегда с тех самых пор,
Чуть истина рождается на свет,
Быки ревут, ее почуя, вслед.
Они не в силах свету помешать.
А могут лишь, закрыв глаза, дрожать
От страха, что вселил в них Пифагор.
Легенда о смерти Пифагора.
Сонную тишину ночного Метапонта прорезал ужасный крик. Послышалось падение на землю тяжелого тела, топот убегающих ног, и все смолкло. Когда ночной караул прибыл на место происшествия, в колеблющемся свете факелов все увидели распростертого на земле старца, и неподалеку от него - мальчика 12 лет с лицом, перекошенным от ужаса.
- Кто это? - спросил начальник караула у мальчика.
- Это Пифагор, - ответил тот.
- Кто такой Пифагор? Среди жителей города нет гражданина с таким именем.
- Мы недавно прибыли из Кротона. Мой господин должен был скрываться от врагов и выходил только ночью. Они выследили его и убили.
- Сколько их было?
- Я этого не успел заметить в темноте. Они отбросили меня в сторону и накинулись на него.
Начальник караула стал на колени и приложил руки к груди старца.
- Конец, - сказал начальник.
“Одному только разуму, как мудрому попечителю, должно вверять свою жизнь”.