Геометрия 8 класс - Технологические карты уроков по учебнику Л. С. Атанасяна - 2015
ТЕОРЕМА ПИФАГОРА - ПЛОЩАДЬ
|
Цель деятельности учителя |
Создать условия для выведения доказательства теоремы Пифагора и ее применения при решении задач |
|||
|
Термины и понятия |
Прямоугольный треугольник, катеты, гипотенуза |
|||
|
Планируемые результаты |
||||
|
Предметные умения |
Универсальные учебные действия |
|||
|
Владеют геометрическим языком, умеют использовать его для описания предметов окружающего мира |
Познавательные: умеют видеть математическую задачу в контексте проблемной ситуации в окружающей жизни. Регулятивные: понимают сущность алгоритмических предписаний и умеют действовать в соответствии с предложенным алгоритмом. Коммуникативные: учитывают разные мнения и стремятся к координации различных позиций в сотрудничестве. Личностные: имеют целостное мировоззрение, соотвтествующее современному уровню развития науки и общественной практики |
|||
|
Организация пространства |
||||
|
Формы работы |
Фронтальная (Ф); индивидуальная (И) |
|||
|
Образовательные ресурсы |
• Учебник. • Задания для фронтальной работы. • Исторические сведения о теореме Пифагора |
|||
|
I этап. Актуализация опорных знаний |
||||
|
Анализ самостоятельной работы |
||||
|
Решение задач по готовым чертежам |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Подготовить учащихся к восприятию новой темы |
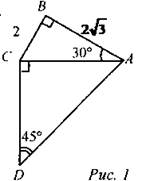
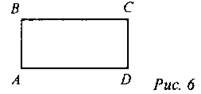
(Ф) 1. Найти SABCD.
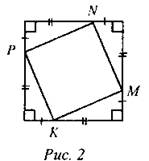
2. Доказать, что MNPK - квадрат.
|
|||
|
II этап. Изучение нового материала |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Показать историческую значимость теоремы Пифагора |
(Ф) Историческая справка (см. Ресурсный материал) |
|||
|
Доказательство теоремы |
||||
|
Цель деятельности |
Совместная деятельность |
|||
|
Предложить учащимся доказательство, отличное от представленного в учебнике |
(Ф) Теорема. В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Данное доказательство основано на разрезании квадратов, построенных на катетах, и укладывании полученных частей на квадрате, построенном на гипотенузе |
|||
|
III этап. Закрепление изученного материала |
||||
|
Цель деятельности |
Деятельность учителя |
Деятельность учащихся |
||
|
На примере решения простейших задач отработать формулу данной теоремы |
(Ф/И) 1. Решить № 483 (а, б), 484 (а, б) (устно). 2. На доске и в тетрадях решить № 487. 3. Самостоятельно решить № 485, 486 |
№ 483 (а, б). 62 + 82 = 100, значит, гипотенуза равна 10. 52 + 62 = 61, значит, гипотенуза равна √61. № 487. Дано: ∆АВС - равнобедренный, АВ = ВС = 17 см, АС = 16 см, BD - высота. Найти: BD.
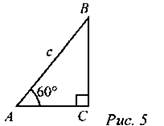
Решение: 1) В равнобедренном треугольнике высота, проведенная к основанию, является медианой, поэтому AD = AC : 2 = 16 : 2 = 8 см. 2) ∆ABD - прямоугольный. По теореме Пифагора: AB2 = AD2 + BD2, откуда BD2= АВ2 - AD2 = 172 - 82 = 225. Так как BD > 0, то BD = 15 см. № 485. Дано: ∆АВС, ∠C = 90°, ∠А = 60°, АВ = с. Найти: ВС.
Решение: 1) Так как ∠В = 30°, то АС = 1/2с. 2) № 486.
а) Если АВ = 5, АС = 13, то AD - ? AD2= АС2 - CD2; AD2= 169 - 25 = 144 AD = 12. б) Если CD = 1,5, АС = 2,5, то ВС - ? ВС2 - АС2 - АВ2’, ВС2 = 6,25 - 2,25 = 4, следовательно, ВС = 2. в) Если BD = 17, ВС = 15, то CD - ? CD2 = BD2 - ВС2, CD2 = 289 - 225 = 64, следовательно, CD = 8 |
||
|
IV этап. Итоги урока. Рефлексия |
||||
|
Деятельность учителя |
Деятельность учащихся |
|||
|
(И/Ф) - С какой теоремой познакомились на уроке? - Составьте синквейн к уроку |
(И) Домашнее задание: подготовить сообщение о жизни Пифагора и его школе |
|||
Ресурсный материал
Историческая справка
Установлено, что теорема Пифагора встречается в вавилонских текстах, написанных за 1200 лет до Пифагора. В математической книге Древнего Китая Чу-пей так говорится о пифагоровом треугольнике со сторонами 3, 4 и 5: “Если прямой угол разложить на составные части, то линия, соединяющая концы его сторон, будет 5, когда основание есть 3, а высота 4”. Кантор (крупнейший немецкий историк математики) считает, что равенство 32 + 42 = 52 было известно уже египтянам еще около 2 300 г. до н. э., во времена царя Аменемхета I (согласно папирусу 6 619, хранящемуся в Берлинском музее). Несколько больше известно о теореме Пифагора у вавилонян. В одном тексте, относимом ко времени Хаммураби, то есть к 2 000 г. до н. э., приводится приближенное вычисление гипотенузы прямоугольного треугольника. Отсюда можно сделать вывод, что в Двуречье умели производить вычисления с прямоугольными треугольниками, по крайней мере в некоторых случаях. У индусов, как и у египтян и вавилонян, геометрия была тесно связана с культом. Весьма вероятно, что теорема о квадрате гипотенузы была известна в Индии уже около XVIII века до н. э.
Основываясь, с одной стороны, на сегодняшнем уровне знаний о египетской и вавилонской математике, а с другой, на критическом изучении греческих источников, голландский математик Ван-дер-Варден сделал следующий вывод: “Заслугой первых греческих математиков, таких как Фалес, Пифагор и пифагорейцы, является не открытие математики, но ее систематизация и обоснование. В их руках вычислительные рецепты, основанные на смутных представлениях, превратились в точную науку”.