График нелинейного уравнения с двумя переменными - РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ - СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Цель: дать представление о графиках некоторых нелинейных уравнений с двумя переменными.

Планируемые результаты: научиться строить графики простейших нелинейных уравнений.

Тип урока: урок-лекция, урок изучения нового материала.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Решите уравнение |2х - 1| = -у² + 6y - 9.

2. При каком значении величины а уравнение 3х² + 5у = 3а² - 13 имеет решение х = а + 1, у = 2а? Найдите это решение.

3. Докажите, что уравнение |2x – 3y + 1| + 8х² = -у² - 1 не имеет решений.

Вариант 2

1. Решите уравнение |3у + 1| = -х² + 4х - 4.

2. При каком значении величины а уравнение 2х + 5у² = 20а² - 9 имеет решение х= 3а, у = 2а - 1? Найдите это решение.

3. Докажите, что уравнение |5х - у + 3| + 2х² = -3у² - 3 не имеет решений.

III. Работа по теме урока

В случае нелинейного уравнения с двумя переменными определение графика остается таким же, как и ранее. Поэтому ограничимся рассмотрением графиков некоторых типичных уравнений.

Пример 1

Рассмотрим уравнение (х - 1)² + (у + 3)² = 0. Очевидно, что при всех значениях переменных х и у квадраты величин х - 1 и y + 3 неотрицательны. Сумма двух неотрицательных величин может равняться нулю только в том случае, когда каждая из них равна нулю, т. е. (х - 1)² = 0 и (у + 3)² = 0. Квадрат величины равняется нулю, если сама величина равна нулю. Получаем уравнения х - 1 = 0 и у + 3 = 0. Решаем эти линейные уравнения с одной переменной и находим х = 1 и у = -3. Итак, решением данного уравнения является только пара чисел (1; -3). Изобразим точку А с такими координатами на плоскости и получим график данного уравнения. В этом случае график представляет собой единственную точку на координатной плоскости.

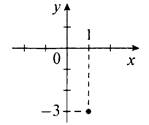
Пример 2

Рассмотрим уравнение ху + х - у - 1 = 0. Сгруппируем члены, разложим его левую часть на множители и получим (xу + х) - (у + 1) = 0, или х(у + 1) - (у + 1) = 0, или (у + 1)(х - 1) = 0. Так как произведение двух множителей равно нулю, то один из таких множителей равен нулю, т. е. у + 1 = 0 (откуда у = -1) или х - 1 = 0 (откуда х = 1). Построим прямые у = -1 (горизонтальная прямая) и х = 1 (вертикальная прямая) на координатной плоскости.

Точки, расположенные на этих прямых, являются решением уравнения. Поэтому построенные прямые — график данного уравнения.

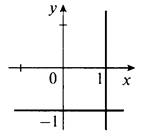
Пример 3

Рассмотрим уравнение ху(у - х²) = 0. Произведение трех множителей равно нулю, если хотя бы один из них равен нулю, т. е. х = 0, или у = 0, или у - х² = 0 (откуда у = х²). Построим прямые х = 0 (ось ординат) и у = 0 (ось абсцисс). Также построим график квадратичной функции у = х² (параболу). Таким образом, график данного уравнения — оси координат и парабола.

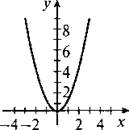
Пример 4

Рассмотрим уравнение (х - 2у)² = х² - 4ху + 4у². Учитывая формулу квадрата разности, получаем, что левая часть уравнения равна правой при всех значениях переменных х и у.

Тогда любая пара чисел (х; у) является решением данного уравнения. Поэтому графиком данного уравнения является координатная плоскость.

Пример 5

Рассмотрим уравнение (3х + 2у - 5)² + |2х - у + 1| + 3 = 0. Левая часть уравнения представляет собой сумму двух неотрицательных величин (3х + 2у - 5)² и |2х - у + 1| и положительного числа 3. Поэтому такая сумма не меньше числа 3 и равняться нулю не может. Следовательно, данное уравнение решений не имеет и его график не существует.

IV. Задания на уроке и на дом

1. Постройте график нелинейного уравнения с двумя переменными:

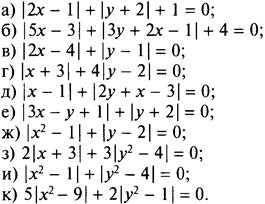
(Ответы: а, б) графика нет; в) точка A (2; 1); г) точка A (-3; 2); д) точка A (1; 1); е) точка A (-1; -2); ж) точки A (1; 2) и В (-1; 2); з) точки A (-3; -2) и В (-3; 2); и) точки A (-1; -2), В (-1; 2), С (1; -2), D (1; 2); к) точки A (-3; -1), В (-3; 1), С (3; -1), D (3; 1).)

2. Постройте график нелинейного уравнения с двумя переменными:

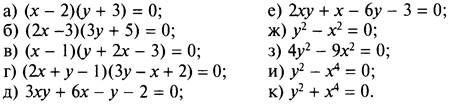
(Ответы: а) прямые х = 2 и у = -3; б) прямые х = 3/2 и у = -5/3; в) прямые х = 1 и у = -2х + 3; г) прямые у = -2х + 1 и у = 1/3х – 2/3; д) прямые х = 1/2 и у = -2; е) прямые x = 3 и у = -1/2; ж) прямые у = -х и у = х; з) прямые у = -1,5 и х = 1,5х; и) параболы у = х² и у = -х²; к) точка А (0; 0).)

3. Постройте график нелинейного уравнения с двумя переменными:

V. Подведение итогов урока