Некоторые системы нелинейных уравнений - РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ - СИСТЕМЫ ЛИНЕЙНЫХ УРАВНЕНИЙ

Цель: познакомить с простейшими системами нелинейных уравнений.

Планируемые результаты: изучить разные способы решения простейших систем нелинейных уравнений.

Тип урока: урок общеметодологической направленности.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (самостоятельная работа).

Вариант 1

1. Постройте график уравнения:

2. На координатной плоскости изобразите множество точек, которое задает неравенство |у + х + 3| ≤ 1.

Вариант 2

1. Постройте график уравнения:

2. На координатной плоскости изобразите множество точек, которое задает неравенство |у - х + 1| ≤ 2.

III. Работа по теме урока

При решении систем нелинейных уравнений используются те же способы, что и при решении систем линейных уравнений: графический способ, способ подстановки и способ сложения.

Пример 1

Решим систему уравнений графическим способом.

Из каждого уравнения системы выразим переменную у через переменную х. Получаем равносильную систему уравнении

Построим график функции у = х² - 1 (парабола I) и график функции у = х + 1 (прямая II). Видно, что графики пересекаются в двух точках А и В. Следовательно, данная система имеет два решения. На рисунке найдем координаты этих точек А (-1; 0) и В (2; 3). Поэтому решения данной системы (-1; 0) и (2; 3).

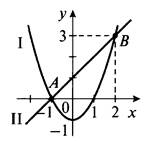
Пример 2

Решим систему уравнений способом подстановки.

Из первого уравнения системы выразим переменную у через переменную х. Получим выражение у = 4 - |х| и подставим его во второе уравнение. Имеем нелинейное уравнение с одним неизвестным: 3(4 - |х|) + х² = 12, или 12 - 3|х| + х² = 12, или х² - 3|х| = 0.

Учтем свойство модуля х² = |х|² и запишем уравнение в виде |х|² - 3|х| = 0. Разложим его левую часть на множители: |х| ∙ (|х| - 3) = 0.

Произведение двух множителей равно нулю, если один из них равен нулю. Имеем уравнения |х| = 0 (так как модуль величины х равен нулю, то и сама величина х = 0) и |х| - 3 = 0 (откуда |х| = 3, тогда величина х = 3 или х = -3). Для каждого значения х по формуле у = 4 - |х| найдем соответствующее значение у. Получаем при х = 0 у = 4, при х = ±3 у = 4 - 3 = 1.

Итак, данная система уравнений имеет три решения (0; 4), (3; 1) и (-3; 1).

Пример 3

Решим систему уравнении способом сложения.

Умножим первое уравнение почленно на число 2, второе уравнение — на число 3 и получим равносильную систему уравнений

Сложим левые и правые части уравнений системы и получим квадратное уравнение с одной переменной 4у² + 9у = 13 или 4у² + 9у - 13 = 0. Решим это уравнение, разложив его левую часть на множители.

Для этого представим 9у в виде 9у = 13у - 4у, сгруппируем члены уравнения и вынесем общие множители за скобки. Получаем 4у² + 13у - 4у - 13 = 0, или у(4у + 13) - (4у + 13) = 0, или (4у + 13)(у - 1) = 0.

Так как произведение множителей равно нулю, то один из множителей равен нулю. Получаем два линейных уравнения 4у + 13 = 0 (корень у = -13/4) и у - 1 = 0 (корень у = 1).

Для каждого значения у найдем соответствующее значение х из второго уравнения 3у - 2|х| = 1 данной системы. При у = -13/4 получаем

Выразим из этого уравнения Так как модуль любой величины — неотрицательное число, то такое уравнение решений не имеет. При у = 1 имеем 3 - 2|x| = 1, откуда |х| = 1. Поэтому сама величина x = 1 или x = -1.

Итак, данная система уравнений имеет два решения (1; 1) и (-1; 1).

Аналогичным способом решают системы уравнений с параметрами.

Пример 4

Решим систему например, методом сложения. Умножим второе уравнение почленно на число -1 и получим

Сложим левые и правые части уравнений системы и получим 2х – у - 2х + ау= 1 - 1 или ау - у = 0.

Вынесем за скобки общий множитель: у(а - 1) = 0.

Так как произведение двух множителей обращается в нуль, то возможны два случая:

1) у = 0; подставив это значение в уравнения данной системы, получаем откуда х = 1/2;

2) а - 1 = 0, т. е. а = 1; подставим это значение а в данную систему и получим

Очевидно, что такая система имеет бесконечно много решений: у = 2х - 1 (где х — любое число).

Итак, если а ≠ 1, то система имеет единственное решение х = 1/2, у = 0; если а = 1, то система имеет бесконечно много решений: х, у = 2х - 1 (где х — любое число).

В некоторых случаях при исследовании корней уравнения его удобно заменить системой уравнений и использовать графический способ.

Пример 5

В зависимости от параметра а определим количество корней уравнения х² - 2х - а = 0.

Запишем данное уравнение в виде х² - 2х = а и рассмотрим функции y = x² - 2x и y = a или систему уравнений

Изобразим графики этих функций (или графики уравнений системы). Графиком функции у = х² - 2х является парабола I. Ее можно построить, составив таблицу значений данной функции. Так как данная функция не зависит от параметра а, то при изменении этого параметра ее график не меняется.

Графиком функции у = а является прямая II, параллельная оси абсцисс и проходящая через точку (0; а). При изменении параметра а прямая II перемещается параллельно самой себе вдоль оси ординат.

На рисунке видно, что при а < -1 парабола и прямая не пересекаются и данное уравнение корней не имеет. При а = -1 парабола и прямая имеют одну общую точку и уравнение имеет один корень. При а > -1 парабола и прямая пересекаются в двух точках и уравнение имеет два корня.

IV. Задания на уроке и на дом

1. Решите систему уравнений всеми изученными способами (графическим способом, способом подстановки, способом сложения):

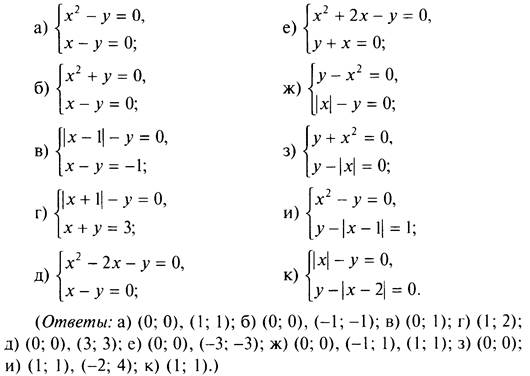
2. Используя графический способ, найдите число решений системы уравнений:

(Ответы: а) решений нет; б) решений нет; в) одно; г) одно; д) два; е) два; ж) два; з) два; и) бесконечно много; к) бесконечно много; л) при а ≠ 1 одно, при а = 1 бесконечно много; м) при а ≠ -2 одно, при а = 1 бесконечно много.)

3. При всех значениях параметра а определите число решений уравнения:

(Ответы: а, б) при а < 0 решений нет, при а = 0 одно, при а > 0 два; в) при а < 3 решений нет, при а = 3 бесконечно много, при а > 3 одно; г) при а < -5 одно, при а = -5 бесконечно много, при а > -5 решений нет; д, е) при а < 0 решений нет, при а = 0 одно, при а > 0 два; ж, з) при а < -4 решений нет, при а = -4 одно, при а > -4 два; и) при а < -1 и а > 1 решений нет, при а = -1 и а = 1 бесконечно много, при -1 < а < 1 одно; к) при а < 3 решений нет, при а = 3 бесконечно много, при а > 3 два; л) при а < 1 решений нет, при а = 7 бесконечно много, при а > 7 два.)

V. Подведение итогов урока