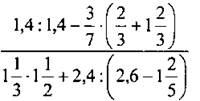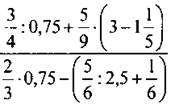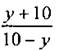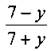Алгебра 7 класс - Технологические карты уроков по учебнику А. Г. Мордковича - 2016
Урок 3. ЧИСЛОВЫЕ И АЛГЕБРАИЧЕСКИЕ ВЫРАЖЕНИЯ - МАТЕМАТИЧЕСКИЙ ЯЗЫК. МАТЕМАТИЧЕСКАЯ МОДЕЛЬ
|
Тип урока: обобщение и систематизация знаний |
||||||
|
Задачи: создать условия для развития умений вычислять значение числового выражения, решать задачи с помощью составления числовых выражений |
||||||
|
Планируемые результаты |
||||||
|
Предметные: научатся находить значения числовых и алгебраических выражений, решать задачи |
Метапредметные: познавательные - ориентироваться на разнообразие способов решения задач; регулятивные - учитывать правило в планировании и контроле способа решения; коммуникативные - учитывать разные мнения и стремиться к координации различных позиций в сотрудничестве |
Личностные: развивать готовность к самообразованию и решению творческих задач |
||||
|
Образовательные ресурсы: 1) Школьный помощник. URL: http://school-assistant.ru/ 2) Видеоуроки. URL: http://interneturok.ru/ |
||||||
|
Организационная структура урока |
||||||
|
Этап урока |
Содержание деятельности учителя |
Содержание деятельности обучающегося (осуществляемые действия) |
Формируемые способы деятельности |
|||
|
1. Организационный этап |
||||||
|
2. Постановка цели и задач урока. Мотивация учебной деятельности учащихся |
||||||
|
3. Проверка домашнего задания |
||||||
|
4. Актуализация знаний |
Теоретические вопросы для учащихся темы “Числовые и алгебраические выражения” РМ |
Отвечают на теоретические вопросы |
Умение работать по заданному алгоритму; доказывать правильность решения с помощью аргументов |
|||
|
5. Обобщение и систематизация знаний |
Организует индивидуальную работу для учащихся, которые не полностью освоили тему (группа А): составить карточки |
У доски |
№ 1.34, 1.38, 1.40, 1.42 |
|||
|
Индивидуально: группа А |
№ 1.35, 1.39, 1.41, 1.43 (а), 1.44(a) |
|||||
|
6. контроль и коррекция знаний |
Самостоятельная работа для учащихся, которые освоили тему (группа В) РМ |
Самостоятельно работают в двух вариантах |
||||
|
7. Рефлексия учебной деятельности на уроке |
- Продолжите высказывание об уроке: • Знания, полученные на уроке, мне необходимы... • Я получил(-а) полезную информацию о том, что... |
Заносят ответы в специальный бланк опроса |
||||
|
8. Домашнее задание |
Задачник: № 1.36, 1.43 (б), 1.44 (б) |
Творческое задание РМ |
||||
Ресурсный материал к уроку 3
1. Теоретические вопросы для учащихся:
• Какое выражение является числовым?
• Как найти значение числового выражения?
• Какое выражение является алгебраическим?
• Как найти значение алгебраического выражения?
• Найти значение выражения 2х2, если х = 1; 2; 0; -3; - 1.
• Найти значение выражения ![]() если а = 2, b = 2; а = 5, b = 2; а = 10, b = 3; а = -6, b = 1.
если а = 2, b = 2; а = 5, b = 2; а = 10, b = 3; а = -6, b = 1.
• Расскажите переместительный закон относительно умножения.
• Какие свойства 1 вам известны?
• Сформулируйте сочетательный закон для сложения.
• Расскажите свойства 0.
• При каких значениях переменных выражение не имеет смысла: ![]()
2. Самостоятельная работа.
|
Вариант I |
Вариант II |
|
1. Данное выражение запишите в виде числового выражения и найдите его значение: |
|
|
Разность произведения чисел |
Частное чисел |
|
2. Вычислите наиболее рациональным способом: |
|
|
|
|
|
3. Выясните, равна дробь нулю или она не имеет смысла: |
|
|
|
|
|
4. Выясните, при каких значениях переменной у данное выражение не имеет смысла: |
|
|
|
|
|
5. При каком значении переменной выражение 12х больше выражения 3х + 5 на 4? |
5. При каком значении переменной сумма выражений 10а и 6 - 8а равна 11? |
Ответы к самостоятельной работе:
|
Задание |
1 |
2 |
3 |
4 |
5 |
|
Вариант I |
-3/20 |
а) 20; б) 35 |
дробь равна нулю |
у = 10 |
х = 1 |
|
Вариант II |
1 |
а) 9,4; б) 30 |
дробь не имеет смысла |
у = -1 |
а = 2, 5 |
3. Творческое задание. Король хочет выстроить 6 крепостей и соединить любые две из них прямолинейной дорогой. Нарисуйте такую схему расположения крепостей и дорог, чтобы на ней было три перекрестка и на любом из них пересекались две дороги.