Поурочные разработки по Математике 5 класс к УМК Н.Я. Виленкина
Среднее арифметическое - Урок 2 - УМНОЖЕНИЕ И ДЕЛЕНИЕ ДЕСЯТИЧНЫХ ДРОБЕЙ - ДРОБНЫЕ ЧИСЛА
Основная дидактическая цель урока: познакомить с решением обратных задач; учить находить среднее арифметическое.
Ход урока
I. Организационный момент
II. Устная работа
1. Индивидуальная работа у доски.
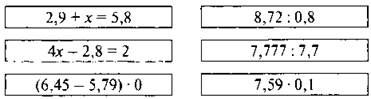
Задание 1. Найдите среднее арифметическое чисел.
18,3; 43,5; 32,1 (31,3.)
Задание 2. Найдите значение выражения.
4,777 : 8,5 = 0,562
Задание 3. Решите уравнение.
8х — 3,2 = 5,6 (х = 1,1.)
2. Фронтальная работа (учащиеся работают вместе с учителем).
(Учитель показывает карточки с заданием, учащиеся называют ответ (возможно использование слайдов презентации).)
3. Коллективная проверка индивидуальной работы у доски.
4. Решите задачу.
В киоске продаются три вида шоколадок и пять сортов мороженого. Сколькими разными способами можно купить шоколадку и мороженое?
— Что это за задача? Докажите.
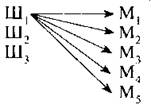
— Сколько различных вариантов мороженого можно выбрать для первой шоколадки? (5.)
— Для второй, третьей?
— Сколько же различных способов выбора существует? (3 ∙ 5 = 15.)
III. Определение темы урока
На доске:
3,5; 3,7; 4,2
60; 65; 85
1,8; 2,5; 6,8
— Какое задание можно придумать для этих чисел? (Учащиеся могут предложить разные варианты заданий, учитель выбирает для выполнения самые интересные, например найти среднее арифметическое этих чисел.)
— Что такое среднее арифметическое?
— Сформулируйте тему урока.
IV. Работа по теме урока
1. Найдите среднее арифметическое чисел.
![]()
— Расскажите, как найти среднее арифметическое нескольких чисел.
2. Найдите среднее арифметическое чисел.
25,6; 28,7; 14,4; 12,8
2,8; 42,3; 7,4; 16,5
32,7; 14,8; 15,3; 21,6
Проверка
![]()
3. С. 227, № 1498.
— Подумайте, что следует из равенства отрезков А В и ВС. (Координата точки В является средним арифметическим координат двух других точек.)
— Чему равна координата точки С? (10,1.)
4. Ответьте на вопросы.
— Как вычислить среднее арифметическое? (Среднее арифметическое = сумма слагаемых: количество слагаемых.)
— Как найти сумму чисел? (Сумма слагаемых = среднее арифметическое ∙ количество слагаемых.)
— Как найти количество слагаемых? (Количество слагаемых = сумма слагаемых : среднее арифметическое.)
— Как можно назвать эти задачи по отношению друг к другу? (Обратные.)
V. Решение задач
1. С. 228, № 1505.
— Какая это задача?
— Можем ли найти сумму этих двух чисел, если известно среднее арифметическое?
— Как это сделать?
— Теперь можем ответить на вопрос задачи?
— Решите задачу.
1) 3,1 ∙ 2 = 6,2 — сумма двух чисел.
2) 6,2 — 3,8 = 2,4 — второе число.
— Подумайте, можно ли решить эту задачу алгебраически.
— Что следует обозначить через х?
Пусть второе число будет х.
Тогда среднее арифметическое этих чисел будет (х + 3,8) : 2.
А по условию среднее арифметическое равно 3,1.
Значит, можем составить уравнение:
(х + 3,8) : 2 = 3,1
х + 3,8 = 3,1 ∙ 2
х + 3,8 = 6,2
х = 6,2 — 3,8
х = 2,4 — второе число.
— Какое решение вам понравилось больше?
2. С. 228, № 1509.
— Какой путь решения выберем? (Алгебраический.)
— Что обозначим через х?
Пусть меньшее число будет х.
Тогда второе число будет 1,5х.
Среднее арифметическое этих чисел (х + 1,5х) : 2.
А по условию среднее арифметическое равно 30.
Значит, можем составить уравнение:
(х + 1,5х) : 2 = 30
2,5х = 30 ∙ 2
2,5х = 60
х = 60 : 2,5
х = 24 — меньшее из чисел.
24 ∙ 1,5 = 36 — второе число.
VI. Повторение изученного материала
1. Найдите среднее арифметическое предметов и существ, которые нас окружают.
• Велосипеда и мотоцикла. (Мопед.)
• Трамвая и поезда. (Электричка.)
• Апельсина и лимона. (Грейпфрут.)
• Туфельки и сапога. (Ботинок.)
• Пианино и баяна. (Аккордеон.)
• Холодильника и вентилятора. (Кондиционер.)
2. С. 288, № 1517 (а, б) (работа в паре).
VIII. Рефлексия
— Как найти сумму чисел, если известны среднее арифметическое и количество слагаемых?
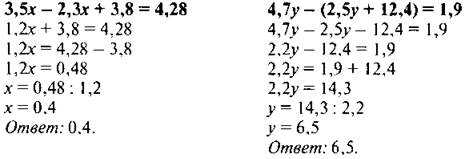
VII. Самостоятельная работа
С. 228, № 1511.
![]()
VIII. Рефлексия
— Как найти сумму чисел, если известны среднее арифметическое и количество слагаемых?
Домашнее задание
С. 230, № 1528, 1532, 1534 (б).