Ещё о рекурсии - Язык Паскаль и начала программирования

Мы уже сталкивались с рекурсией, посвятив этому явлению § 2.4.5; к сожалению, на тот момент мы знали слишком мало и не могли разобрать примеры, в которых выразительная мощь рекурсии раскрылась бы в полной мере. Сейчас, умея работать со строками и списками, получив представление о деревьях и имея в целом больше опыта, мы вернёмся к обсуждению рекурсивного программирования и попытаемся дать более адекватное представление о его возможностях.

2.14.1. Взаимная рекурсия

Ранее мы упоминали о том, что рекурсия может быть взаимной; в простейшем случае одна подпрограмма вызывает другую, а вторая — снова первую. При этом возникает небольшая техническая проблема: одна из двух подпрограмм, участвующих во взаимной рекурсии, должна быть в программе описана раньше второй, но в ней должен (по условию) присутствовать вызов второй подпрограммы — то есть вызов подпрограммы, которая будет описана позже. Проблема тут в том, что компилятор пока что не знает имени второй подпрограммы и, как следствие, не позволяет это имя использовать, то есть вызов второй подпрограммы из первой приведёт к ошибке компиляции.

Для решения этой проблемы в Паскале введено понятие предварительного объявления (декларации) подпрограмм. В отличие от /подпрограмма!описание│описания подпрограммы, декларация только сообщает компилятору, что позже в тексте программы появится подпрограмма (процедура или функция) с таким-то именем, причём она будет иметь такие-то параметры, а для функций — такой-то тип возвращаемого значения. Больше никакой информации декларация компилятору не даёт, то есть в ней не пишется ни тело подпрограммы, ни секция локальных описаний. Вместо всего этого сразу после заголовка, сформированного обычным путём, ставится ключевое слово forward и точка с запятой, например:

Такие декларации позволяют не писать тело подпрограммы, к чему мы можем быть пока что не готовы, как правило, из-за того, что пока в программе описаны не все подпрограммы, вызываемые из этого тела. Декларация сообщает компилятору, во-первых, имя подпрограммы, и, во-вторых, всю информацию, необходимую для проверки корректности вызова таких подпрограмм и для генерации машинного кода, осуществляющего вызовы (это может потребовать преобразований типов выражений, так что типы параметров подпрограммы в точке её вызова должны быть известны компилятору не только для проверки корректности).

При построении взаимной рекурсии мы сначала в программе приводим декларацию (со словом forward) первой из подпрограмм, участвующих в ней, затем описываем (полностью, с телом) вторую из этих подпрограмм, и уже затем приводим полное описание первой. При этом в обоих телах компилятору видны имена обеих подпрограмм и вся информация, нужная для их вызова, что нам, собственно, и требовалось.

Ясно, что задекларированная подпрограмма должна быть позже описана; если этого не сделать, при компиляции произойдёт ошибка.

2.14.2. Ханойские башни

Задачу о ханойских башнях мы рассматривали во вводной части книги при обсуждении понятия алгоритма (см. § 1.5.5). Тогда же мы пообещали продемонстрировать текст этой программы сначала на Паскале, а затем и на Си; сейчас самое время исполнить первую часть обещания.

Напомним, что в этой задаче даны три стержня, на один из которых надето N плоских дисков, различающихся по размеру, внизу самый большой диск, сверху самый маленький. За один ход можно переместить один диск с одного стержня на другой, при этом можно класть только меньший диск сверху на больший; на пустой стержень можно поместить любой диск. Брать сразу несколько дисков нельзя. Цель в том, чтобы за наименьшее возможное число ходов переместить все диски с одного стержня на другой, пользуясь третьим в качестве промежуточного.

Как мы уже обсуждали в § 1.5.5, самое простое и известное решение строится в виде рекурсивной процедуры переноса заданного количества п дисков с заданного исходного стержня на заданный целевой с использованием заданного промежуточного (его можно было бы вычислить, но проще получить его номер параметром процедуры); в качестве более простого случая выступает перенос n — 1 дисков, а в качестве базиса рекурсии — вырожденный случай n = 0, когда ничего никуда переносить уже не нужно.

В роли исходных данных для нашей программы выступает общее число дисков, которое мы для удобства получим в качестве параметра командной строки⁴⁵. Рекурсивную реализацию алгоритма оформим в виде процедуры, которая для наглядности получает четыре параметра: номер исходного стержня (source), номер целевого стержня (target), номер промежуточного стержня (transit) и количество дисков (n). Саму процедуру назовём “solve”. В ходе работы она будет печатать строки вроде “1: 3 -> 2” или “7: 1 -> 3”, которые будут означать, соответственно, перенос диска № 1 с третьего стержня на второй и диска № 7 с первого на третий. Главная программа, преобразовав параметр командной строки в число⁴⁶, вызовет подпрограмму solve с параметрами 1, 3, 2, N, в результате чего задача будет решена. Текст программы будет таким:

Отметим, что процедура, решающая задачу, состоит всего из восьми строк, три из которых служебные.

Попробуем теперь обойтись без рекурсии. Для начала припомним алгоритм, который мы приводили ранее: на нечётных ходах самый маленький диск переносится “по кругу”, причём при чётном общем количестве дисков — в “прямом” порядке, то есть 1 → 2 → 3 → 1 → ..., а при нечётном — в “обратном” порядке, 1 → 3 → 2 → 1 → ...; что касается чётных ходов, то на них мы не трогаем самый маленький диск, в результате чего ход оказывается определён однозначно.

Попытка реализовать этот алгоритм в виде программы наталкивается на неожиданное препятствие. Для человека действие вроде “посмотреть на стержни, найти самый маленький диск и, не трогая его, сделать единственный возможный ход” настолько просто, что мы выполняем такую инструкцию, ни на секунду не задумавшись; в программе же придётся помнить, на каком стержне находятся в настоящий момент какие диски, и выполнять множество сравнений, учитывая ещё и то, что стержни могут оказаться пустыми.

В архиве примеров к этой книге вы найдёте соответствующую программу в файле с именем hanoi2.pas. Здесь её текст мы не приводим с целью экономии места. Отметим только, что для хранения информации о расположении дисков на стержнях мы в этой программе воспользовались тремя односвязными списками, по одному на каждый стержень, причём в первый список в начале работы внесли в обратном порядке числа от n до 1, где n — количество дисков; для хранения указателей на первые элементы этих списков мы используем массив из трёх соответствующих указателей. Для решения задачи мы запускаем цикл, который выполняется до тех пор, пока хотя бы один “диск” (то есть элемент списка) присутствует в списках № 1 и № 2. Движение самого маленького диска мы на нечётных ходах просто вычисляем по формулам, для чего используем номер хода. В частности, номер стержня, с которого нужно забрать диск, при чётном общем количестве дисков вычисляется так:

а при нечётном так (turn означает номер хода):

Гораздо сложнее обстоят дела с чётными ходами. Для вычисления такого хода нужно, во-первых, узнать, на каком из стержней располагается самый маленький диск, и исключить этот стержень из рассмотрения. Затем для оставшихся двух стержней нужно определить, в каком направлении между ними переносится диск, с учётом того, что один из них может оказаться пустым (и тогда диск переносится на него с другого стержня), либо они могут оба содержать диски, тогда меньший из дисков переносится на другой стержень, где находится больший. Тело подпрограммы, в которую вынесены эти действия, несмотря на их кажущуюся простоту, заняло 15 строк.

Общая длина программы составила 111 строк (против 27 для рекурсивного решения), если же мы отбросим пустые и служебные строки, а также и текст главной части программы, который в обоих случаях практически один и тот же (отличаются только параметры вызова процедуры solve), и посчитаем только значимые строки, реализующие решение, то в рекурсивном варианте таких строк было восемь (текст подпрограммы solve), тогда как в новом решении их получилось 87. Иначе говоря, решение стало сложнее более чем на порядок!

Теперь попробуем сделать решение без рекурсии, которое не использует вышеизложенный “хитрый” алгоритм. Вместо этого вспомним, что для перемещения всех дисков с одного стержня на другой нужно для начала переместить все диски, кроме самого большого, на промежуточный стержень, затем переместить самый большой диск на целевой стержень и, наконец, переместить все остальные стержни с промежуточного на целевой. Несмотря на то, что описание алгоритма очевидным образом рекурсивно, реализовать его можно без рекурсии; в принципе, это справедливо для любого алгоритма, то есть рекурсию всегда можно заменить циклом, вопрос лишь в том, насколько это сложно.

Трудность в том, что мы в каждый момент должны помнить, что мы сейчас куда переносим и с какой целью. Например, в процессе решения задачи для четырёх дисков мы в какой-то момент переносим первый (самый маленький) диск со второго стержня на третий, чтобы перенести два диска со второго стержня на первый, чтобы иметь возможность перенести третий диск со второго стержня на третий, чтобы перенести три диска со второго стержня на третий (поскольку четвёртый диск мы туда уже перенесли), чтобы перенести все четыре диска с первого на третий стержень. Это можно несколько удобнее расписать “с конца”:

• мы решаем задачу переноса четырёх дисков с первого стержня на третий, причём уже убрали все диски на второй стержень, перенесли четвёртый диск на третий стержень и теперь находимся в процессе переноса туда всех остальных дисков, т. е.

• решаем задачу переноса трёх дисков со второго стержня на третий, причём сейчас как раз пытаемся освободить третий диск, чтобы потом его перенести на третий стержень, для чего

• решаем задачу переноса двух дисков со второго стержня на первый, причём сейчас как раз пытаемся освободить второй диск, чтобы потом перенести его на первый стержень, для чего

• переносим первый диск со второго стержня на третий.

Очевидно, что здесь мы имеем дело с задачами, которые характеризуются информацией о том, сколько дисков мы хотели перенести, откуда, куда, а также в каком состоянии у нас с этим дела. Задач у нас переменное количество, так что придётся использовать какую-то динамическую структуру данных, проще всего, видимо, обычный список. Для каждой задачи придётся хранить количество дисков и два номера стержней, а также состояние дел, причём таких состояний можно выделить три:

1. мы ещё вообще ничего не делали; следующее действие в этом случае — расчистить самый большой из наших дисков, убрав все, которые меньше его, на промежуточный стержень;

2. мы уже расчистили самый большой диск, теперь его надо перенести, а затем перенести на него все диски, которые меньше его;

3. мы уже решили задачу, так что её можно убрать из списка.

В принципе, одно из этих состояний (последнее) можно было бы “сэкономить”, но это пошло бы в ущерб ясности программы. Для обозначения состояний мы воспользуемся перечислимым типом на три возможных значения, обозначающих, что нужно делать следующим действием, когда мы снова видим данную задачу:

Опишем тип для звеньев списка задач:

и два указателя, рабочий и временный:

Для решения поставленной проблемы нам нужно перенести все диски (n штук) с первого стержня на третий. Оформим это в виде задачи и занесём получившуюся задачу в список (единственным элементом), учитывая, что мы ещё ничего не сделали, так что в качестве состояния задачи укажем StClearing:

Далее организуется цикл, работающий до тех пор, пока список задач не опустеет. На каждом шаге цикла выполняемые действия зависят от того, в каком состоянии находится задача, стоящая в начале списка. Если она в состоянии StClearing, то в случае, когда эта задача требует переноса более чем одного диска, нужно добавить ещё одну задачу — для переноса n — 1 дисков на промежуточный стержень; если текущая задача создана для переноса только одного диска, этого делать не надо. В обоих случаях сама текущая задача переводится в следующее состояние, StLargest, то есть когда мы её увидим в следующий раз (а это произойдёт либо после переноса всех меньших дисков, либо, если диск всего один, то прямо на следующем шаге), нужно будет перенести самый большой из дисков, подразумеваемых данной задачей, и перейти к финальной стадии.

Если на вершине списка находится задача в состоянии StLargest, то первое, что мы делаем — это переносим самый большой из дисков, на которые данная задача распространяется; номер этого диска совпадает с их количеством в задаче. Под словами “переносим диск” мы в данном случае подразумеваем, что мы просто печатаем соответствующее сообщение. После этого, если дисков в задаче больше одного, нужно добавить новую задачу по переносу всех меньших дисков с промежуточного стержня на целевой; если диск всего один, этого делать не надо. В любом случае текущая задача переводится в состояние StFinal, чтобы, когда мы её увидим в начале списка в следующий раз, её можно было ликвидировать.

Очередная возникающая перед нами проблема — это вычисление номера промежуточного стержня; для этого мы предусмотрели в программе отдельную функцию:

С использованием этой функции основной цикл “решения задач” выглядит так:

Полностью текст программы вы найдёте в файле hanoiS.pas; отметим, что его размер — 90 строк, из которых 70 — значащие строки реализации процедуры solve (включая вспомогательные подпрограммы). Получилось несколько лучше, чем в предыдущем случае, но всё равно в сравнении с рекурсивным решением разница почти на порядок.

2.14.3. Сопоставление с образцом

Рассмотрим такую задачу. Даны две строки символов, длина которых заранее неизвестна. Первую строку мы рассматриваем как со поставляемую, вторую — как образец. В образце символ ’?’ может сопоставляться с произвольным символом, символ ’*’ — с произвольной подцепочкой символов (возможно, пустой), остальные символы обозначают сами себя и сопоставляются только сами с собой. Так, образцу ’abc’ соответствует только строка ’abc’; образцу ’a?c’ соответствует любая строка из трёх символов, начинающаяся на ’a’ и заканчивающаяся на ’c’ (символ в середине может быть любым). Наконец, образцу ’a*’ соответствует любая строка, начинающаяся на ’a’, ну а образцу ’*a*’ соответствует любая строка, содержащая букву ’a’ в любом месте. Необходимо определить, соответствует ли (целиком) заданная строка образцу.

Алгоритм такого сопоставления, если при этом можно использовать рекурсию, окажется достаточно простым. На каждом шаге мы рассматриваем оставшуюся часть строки и образца; сначала эти оставшиеся части совпадают со строкой и образцом, затем, по мере продвижения алгоритма, от них отбрасываются символы, стоящие в начале, и мы предполагаем, что для уже отброшенных символов сопоставление прошло успешно. Первое, что нужно сделать в начале каждого шага — это проверить, не кончился ли у нас образец. Если он кончился, то результат зависит от того, кончилась ли при этом и строка тоже. Если кончилась, то мы фиксируем положительный результат сопоставления, если не кончилась — констатируем неудачу; действительно, с пустым образцом можно сопоставить только пустую строку.

Если образец ещё не кончился, проверяем, не находится ли в его начале (то есть в первом символе остатка образца) символ ’*’. Если нет, то всё просто: мы производим сопоставление первых символов строки и образца; если первый символ образца не является символом ’?’ и не равен первому символу строки, то алгоритм на этом завершается, констатируя неудачу сопоставления, в противном случае считаем, что очередные символы образца и строки успешно сопоставлены, отбрасываем их (то есть укорачиваем остатки обеих строк спереди) и возвращаемся к началу алгоритма.

Самое интересное происходит, если на очередном шаге первый символ образца оказался символом ’*’. В этом случае нам нужно последовательно перебрать возможности сопоставления этой “звёздочки” с пустой подцепочкой строки, с одним символом строки, с двумя символами и т. д., пока не кончится сама строка. Делаем мы это следующим образом. Заводим целочисленную переменную, которая будет у нас обозначать текущий рассматриваемый вариант. Присваиваем этой переменной ноль (начинаем рассмотрение с пустой цепочки). Теперь для каждой рассматриваемой альтернативы отбрасываем от образца один символ (звёздочку), а от строки — столько символов, какое сейчас число в нашей переменной. Полученные остатки пытаемся сопоставить, используя для этого вызов той самой подпрограммы, которую мы сейчас пишем, то есть производим рекурсивный вызов “самих себя”. Если результат вызова — “истина”, то мы на этом завершаемся, тоже вернув “истину”. Если же результат — “ложь”, то мы проверяем, можно ли ещё увеличивать переменную (не выйдем ли мы при этом за пределы сопоставляемой строки). Если увеличиваться уже некуда, завершаем работу, вернув “ложь”. В противном случае возвращаемся к началу цикла и рассматриваем следующее возможное значение длины цепочки, сопоставляемой со “звёздочкой”.

Весь этот алгоритм мы реализуем в виде функции, которая будет получать в качестве параметров две строки, сопоставляемую и образец, и два целых числа, показывающих, с какой позиции следует начинать рассмотрение той и другой строки. Возвращать наша функция будет значение типа boolean: true, если сопоставление удалось, и false, если не удалось. Принимая во внимание, что значения типа string занимают в памяти достаточно много места (256 байт) и что наша функция постоянно выполняет вызовы самой себя, строки мы ей будем передавать как var-параметры, избегая таким образом их копирования. Функцию мы назовём Matchldx, поскольку она решает задачу сопоставления, но не просто над строками, а над “остатками” заданных строк, начиная с заданных индексов.

Исходную задачу будет решать другая функция, которую мы назовём просто Match; в неё будут передаваться только две строки, и всё. Тело этой функции будет состоять из вызова функции Matchldx с теми же двумя строками и со значениями индексов, равными единице, что означает рассмотрение обеих строк с их начала. В этот раз мы опишем строковые параметры как обычные параметры-значения. Дело в том, что функция Match вызывается один раз, никаких рекурсивных вызовов для неё не предусмотрено, так что здесь копирование строк при вызове не столь страшно; с другой стороны, если её параметры объявить как параметры-переменные, то мы потеряем возможность вызывать эту функцию с параметрами, которые не являются переменными — например, не сможем задать образец в виде строкового литерала, а это часто бывает нужно. Используя параметры-значения для Match, мы можем для Matchldx совершенно спокойно использовать параметры-переменные, ведь она будет вызываться только из Match — и, стало быть, работать с её локальными переменными. Иначе говоря, если нам понадобится сопоставить строку с образцом, мы обратимся к нашим функциям, они для себя сделают копии обеих строк, а дальше будут работать только с этими копиями.

Для тестирования добавим к нашей программе заголовок и главную часть, которая берёт строку и образец из параметров командной строки. Результат получится такой:

При работе с этой программой учтите, что символы “*” и “?” воспринимаются командным интерпретатором специфически: он тоже считает своим долгом произвести некое сопоставление с образцом (подробности см. в § 1.4.5). Самый простой и надёжный способ избежать неприятностей со спецсимволами — взять ваши параметры в апострофы, внутри них командный интерпретатор никакие подстановки не выполняет; сами апострофы при передаче вашей программе исчезнут, то есть вы не увидите их в составе строк, возвращённых функцией ParamStr. Сеанс работы с программой match_pt может выглядеть так:

и так далее.

2.14.4. Рекурсия при работе со списками

Как уже упоминалось, односвязный список рекурсивен по своей сути: можно считать, что список либо пустой, либо состоит из первого элемента и списка. Это свойство можно использовать, обрабатывая односвязные списки с помощью рекурсивных подпрограмм, при этом почти всегда базисом рекурсии оказывается пустой список. Пусть, например, у нас имеется простейший список целых чисел, состоящий, как и в предыдущих примерах, из элементов типа item:

Начнём с простого подсчёта суммы чисел в таком списке. Конечно, можно пройти по списку циклом, как мы это уже неоднократно делали:

Теперь попробуем воспользоваться тем фактом, что сумма пустого списка равна нулю, а сумма непустого равна сумме его остатка, к которой прибавлен первый элемент. Новая (рекурсивная) реализация функции ItemListSum получится такой:

По правде говоря, если в вашем списке хранится несколько миллионов записей, то так лучше не делать, потому что может не хватить стека, но, с другой стороны, для хранения миллионов записей списки обычно не используются. Если же переполнение стека вам не угрожает, то удачные рекурсивные решения, как это ни странно, могут работать даже быстрее, чем “традиционные” циклы.

Рассмотрение примеров мы продолжим процедурой удаления всех элементов списка. Как это делается циклически, мы подробно рассмотрели ранее; теперь заметим, что для удаления пустого списка ничего делать не нужно, тогда как для удаления непустого списка следует освободить память от его первого элемента и удалить его остаток. Конечно, удаление остатка следует произвести первым, чтобы при удалении первого элемента не потерять указатель на этот самый остаток. Пишем:

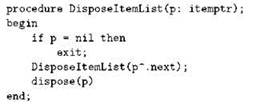
Нельзя сказать, чтобы мы здесь сильно выиграли в объёме кода, но то, что рекурсивное удаление списка проще прочитать, несомненно: для понимания здесь даже не требуется рисовать диаграммы.

Рассмотрим теперь пример посложнее. Мы рассматривали пример кода, вставляющего новый элемент в список целых чисел, отсортированный по возрастанию, с сохранением сортировки. Для циклического решения этой задачи нам потребовался указатель на указатель. Заметим теперь, что, коль скоро нам потребовалось вставить новый элемент в отсортированный список, у нас возможны три случая:

• список пустой — нужно вставить в него элемент первым;

• список непустой, причём его первый элемент больше, чем вставляемый — нужно вставить новый элемент в начало;

• список непустой, а первый элемент меньше или равен вставляемому — нужно произвести его вставку в остаток списка.

Как мы уже обсуждали, если указатель на первый элемент списка передать в подпрограмму как параметр-переменную, то такая подпрограмма сможет вставлять и удалять элементы в любом месте списка, в том числе и в начале. Кроме того, полезно будет припомнить, что вставка элемента в пустой односвязный список и вставка элемента в начало непустого списка производятся абсолютно одинаково, что позволяет объединить два первых случая в один, который как раз и послужит базисом рекурсии. Заметим, что роль “указателя на первый элемент” для того списка, который является остатком исходного, играет поле next в первом элементе исходного списка. С учётом всего этого процедура, вставляющая новый элемент в отсортированный список с сохранением сортировки, будет выглядеть так:

Сравните это с кодом, приведённым ранее, и пояснениями к нему. Комментарии, как говорится, излишни.

2.14.5. Работа с двоичным деревом поиска

Обсуждая двоичные деревья в § 2.13.8, мы намеренно не приводили примеров кода для работы с ними, оставив этот вопрос до обсуждения рекурсивных методов работы. Если в случае с односвязными списками применение рекурсии способно несколько облегчить работу, то для деревьев речь должна идти скорее не о том, чтобы работу облегчить, а о том, чтобы сделать её возможной.

Для примера рассмотрим двоичное дерево поиска, содержащее целые числа типа longint, которое может состоять, например, из таких узлов:

Для работы с ним нам потребуется указатель, который часто называют корнем дерева; впрочем, корнем не менее часто называют начальный узел сам по себе, а не указатель на него. Из контекста обычно легко понять, о чём идёт речь. Корневой указатель опишем так:

Теперь мы можем приступать к описанию основных действий с деревом. Поскольку нам придётся активно использовать рекурсию, мы каждое действие будем оформлять в виде подпрограммы. Чтобы приблизительно понять, как всё это будет выглядеть, для начала предположим, что дерево уже построено, и напишем функцию, которая вычисляет сумму значений во всех его узлах. Для этого заметим, что для пустого дерева такая сумма, очевидно, равна нулю; если же дерево непустое, то для подсчёта искомой суммы нужно будет вычислить для начала сумму левого поддерева, потом сумму правого поддерева, сложить их между собой и прибавить число из текущего узла. Поскольку левое и правое поддеревья представляют собой такие же деревья, как и дерево целиком, только с меньшим количеством узлов, мы можем для вычисления сумм поддеревьев воспользоваться той же функцией, которую пишем:

Собственно говоря, практически всё, что мы делаем с деревом, строится по этой же схеме: в качестве вырожденного случая для базиса рекурсии используется пустое дерево, а дальше делаются рекурсивные вызовы для левого и/или правого поддерева. Продолжим наш набор примеров подпрограммой, добавляющей в дерево новый элемент; когда дерево пустое, необходимо создать элемент “прямо здесь”, то есть изменить тот указатель, который служит для данного дерева корневым; с учётом этого указатель в процедуру будем передавать как параметр-переменную. Если же дерево не пусто, то есть, по крайней мере, существует его корневой элемент, то тогда возможны три случая. Во-первых, добавляемый элемент может быть строго меньше того, который находится в корневом элементе; тогда добавление следует произвести в левое поддерево. Во-вторых, он может быть строго больше, и тогда следует использовать правое поддерево. Третий случай портит нам всю картину, добавляя особый случай: числа могут оказаться равными. В зависимости от задачи в такой ситуации возможны различные варианты дальнейших действий: иногда при совпадении ключей выдают ошибку, иногда увеличивают какой-нибудь счётчик, чтобы показать, что данный ключ заносился на один раз больше, иногда вообще ничего не делают. Мы остановимся на том, что сообщим вызывающему о невозможности выполнения добавления; для этого нашу подпрограмму оформим как функцию типа boolean и сделаем так, чтобы она возвращала “истину”, когда значение успешно добавлено, и “ложь”, когда возник конфликт ключей. Получится следующее:

Если попробовать написать функцию, определяющую, есть ли в данном дереве заданное число, получится нечто очень похожее:

Схожесть двух подпрограмм не случайна, ведь в обоих случаях производится поиск. В принципе, для поиска нужной позиции можно написать одну обобщённую функцию, через которую затем описать и добавление, и обычный поиск: такая функция будет по заданному дереву и значению искать позицию в дереве, где должен находиться (но не обязательно находится) узел с таким значением. Как уже можно догадаться, эта “позиция” есть не что иное, как адрес того указателя, который указывает или должен указывать на соответствующий узел. Поскольку этот адрес указателя будет служить возвращаемым значением функции, соответствующий тип значения нам придётся описать и снабдить именем:

Отметим, во-первых, что такая функция должна в некоторых случаях возвращать адрес того указателя, который ей дали — если дерево оказалось пустым, а равно и в том случае, если корневой элемент дерева содержит искомое число. Для того, чтобы вернуть такой адрес, его надлежит по меньшей мере знать, и для этого мы указатель будем передавать как параметр-переменную; имя такого параметра, как мы помним, на время выполнения подпрограммы становится синонимом переменной, использованной в качестве параметра в точке вызова, так операция взятия адреса, применённая к имени параметра, как раз и даст нам адрес этой переменной. Во-вторых, случаи пустого дерева и равенства искомого значения значению в корневом узле теперь можно объединить: в случае равенства мы нашли позицию, где соответствующее число находится, а в случае пустого поддерева — позицию, где оно должно было бы находиться. Различить эти два случая сможет вызывающий, проверив, чему равен указатель, расположенный по полученному из функции адресу: nil или нет. Текст функции получается такой:

Используя эту функцию, две ранее написанные подпрограммы мы можем переписать по-новому, при этом они станут заметно короче:

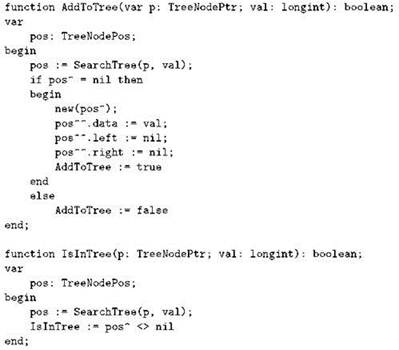
Небольшую демонстрационную программу, использующую эти функции, вы найдёте в файле treedemo.pas. К сожалению, мы вынуждены напомнить о серьёзном недостатке двоичных деревьев поиска: при неудачном порядке занесения в них хранимых значений дерево может получиться несбалансированным. Существует несколько подходов к такому построению двоичного дерева поиска, при котором разбалансировка либо вообще не возникает, либо оперативно устраняется, но рассказ о них выходит далеко за рамки нашей книги.

На случай возникновения у читателя непреодолимого желания освоить алгоритмы балансировки деревьев возьмём на себя смелость обратить его внимание на несколько книг, в которых соответствующие вопросы подробно разобраны. Начать стоит с учебника Н. Вирта “Алгоритмы к структуры данных” [8]; изложение в этой книге отличается лаконичностью и понятностью, поскольку рассчитано на начинающих. Если этого не хватило, попробуйте воспользоваться огромной по объёму книгой Кормена, Лейзерсона и Ривеста [9]; наконец, для сильных духом существует ещё и четырёхтомник Дональда Кнута, третий том которого [10] содержит подробный анализ всевозможных структур данных, ориентированных на сортировку и поиск.

В качестве упражнения рискнём предложить читателю попробовать написать подпрограммы для работы с деревьями без использования рекурсии. Отметим, что поиск в дереве при этом реализуется сравнительно просто и немного похож на вставку элемента в нужное место односвязного списка, как это было показано в § 2.13.6. Гораздо сложнее оказывается алгоритм обхода дерева, который нужен в том числе для подсчёта суммы элементов списка; но и здесь мы уже успели рассмотреть нечто похожее, когда решали задачу о ханойских башнях (§ 2.14.2). В программе, обсуждение которой мы начали ранее, нам приходилось запоминать, каким путём мы пришли к необходимости сделать то или иное действие, а затем возвращаться обратно и продолжать прерванную деятельность. При обходе дерева нужно, по сути, то же самое: для каждого узла, в который мы попали, мы вынуждены помнить то, откуда мы в него попали, а также то, что уже успели в этом узле сделать, или, точнее, что нам предстоит делать, когда мы снова вернёмся к этому узлу.

Если не получится — ничего страшного, эта задача довольно сложная; мы вернёмся к ней, когда будем изучать язык Си.