Адреса, указатели и динамическая память - Язык Паскаль и начала программирования

До сих пор мы использовали только переменные, задаваемые во время написания программы; поскольку переменная есть не более чем область памяти, это, в частности, означает, что именно во время написания программы мы полностью определяли, сколько памяти наша программа будет использовать во время исполнения.

Между тем, во время написания программы мы можем попросту не знать, сколько нам потребуется памяти. Учебные задачи часто специально формулируются так, чтобы проблема размера не возникала: например, нам могут сказать, что каких-нибудь чисел может быть сколько угодно, но не больше 10000, или что строки могут быть произвольной длины, но никак не длиннее 255 символов, или ещё что-нибудь в таком духе; на практике ограничения подобного рода могут оказаться неприемлемыми. Такова, например, задача, решаемая стандартной программой sort: эта программа прочитывает некий текст (из файла или из стандартного потока ввода), после чего выполняет сортировку и выдаёт строки прочитанного текста в отсортированном порядке. Программа не накладывает никаких ограничений ни на длину отдельной строки, ни на их общее количество; лишь бы хватило памяти. Стоит отметить, что памяти в разных системах может быть разное количество; программа sort написана без каких-либо предположений о том, сколько памяти ей будет доступно, и пытается занять столько, сколько ей необходимо для сортировки конкретного текста. Если для поданного ей конкретного текста не хватило памяти в конкретной системе, программа, конечно, не сработает; но если памяти хватит, она успешно выполнит свою задачу, причём лишней памяти в ходе выполнения не займёт.

Освоение адресов и указателей как раз и позволит нам писать такие программы, которые сами во время исполнения определяют, сколько памяти нужно использовать. Такая возможность появляется благодаря динамическим переменным, которые, в отличие от обычных переменных, не описываются в тексте программы, а создаются во время её выполнения. При этом было бы неправильно полагать, что указатели нужны только для этого; их область применения гораздо шире.

Возможно, эта глава покажется вам самой сложной; к сожалению, может получиться и так, что вы вообще не поймёте, о чём здесь идёт речь. Указатели не входят в школьную программу информатики, причём, судя по всему, причина этого не в том, что школьники не смогут их освоить, а в том, что указатели превышают возможности большинства учителей.

Между тем, позднее нам предстоит изучение языка Си, в котором, в отличие от Паскаля, практически ничего нельзя сделать, не понимая концепцию адресов и указателей. Паскаль в этом плане более лоялен к ученикам, он позволяет писать довольно сложные программы, не прибегая к указателям. Собственно говоря, мы как раз и выбрали Паскаль в качестве первого учебного языка, чтобы сначала научиться программировать, а потом, когда настанет подходящий момент, изучить заодно и указатели — и тем самым подготовиться к премудростям Си. Увы, без материала этой главы выбор Паскаля теряет всякий смысл, с тем же успехом можно было бы изучать любой другой язык. Ранее мы советовали пропустить параграф или даже целую главу, если она окажется слишком сложной, и вернуться к ней позже; для главы, посвящённой указателям, мы этого порекомендовать не можем.

Если материал, изложенный в этой главе, окажется вам не по силам, можно посоветовать либо найти кого-то, кто сможет вам помочь разобраться, либо вообще отложить на какое-то время освоение новых инструментов и попытаться писать программы с помощью всего того, что вы уже освоили. Возможно, спустя несколько месяцев и полдюжины написанных и отлаженных программ глава про указатели не покажется вам столь сложной.

Кроме того, вы можете взять следующий том, попробовать прочитать третью часть нашей книги, которая посвящена программированию на уровне машинных команд с помощью языка ассемблера, и после этого возобновить попытки освоения указателей. Чего точно не стоит делать — это пытаться, так и не поняв указатели, изучать Си; всё равно не получится.

2.13.1. Что такое указатель

Напомним для начала несколько базовых утверждений. Во-первых, память компьютера состоит из одинаковых ячеек, каждая из которых имеет свой адрес. В большинстве случаев адрес — это просто целое число, но не всегда; на некоторых архитектурах адрес может состоять из двух чисел, и теоретически можно себе представить адреса, имеющие ещё более сложную структуру. Что можно уверенно сказать, так это то, что адрес есть некая информация, позволяющая однозначно идентифицировать ячейку памяти.

Во-вторых, мы часто пользуемся не отдельными ячейками памяти, а некими наборами ячеек, идущих подряд, которые мы называем областями памяти. В частности, любая переменная есть область памяти (переменные некоторых типов, таких как char или byte, занимают ровно одну ячейку, что можно считать частным случаем области). Адресом области памяти считается адрес первой ячейки этой области.

Как и другую информацию, адреса можно хранить в памяти, то есть одна область памяти может содержать (хранить) адрес другой области памяти. Многие языки программирования высокого уровня, включая Паскаль, предусматривают специальный тип или семейство типов выражений, которые соответствуют адресам; переменная такого типа, то есть переменная, в которой хранится адрес (например, адрес другой переменной) как раз и называется указателем.

Всю премудрость указателей и адресов можно выразить всего двумя короткими фразами:

Указатель — это переменная, в которой хранится адрес

Утверждение вида “А указывает на В” означает “А содержит адрес В”

На практике довольно часто допускают терминологические вольности, путая понятия адреса и указателя; например, можно услышать, что некая функция “возвращает указатель”, тогда как на самом деле она возвращает, естественно, не переменную, а значение, то есть адрес, а не указатель. Точно так же довольно часто про адрес (а не про указатель) говорят, что он на что-то указывает, хотя адрес, конечно же, не указывает на переменную, а является её свойством. Хотя формально утверждения такого вида не вполне верны, никакой путаницы они, как ни странно, не порождают: всегда остаётся понятным, что имеется в виду.

2.13.2. Указатели в Паскале

В большинстве случаев в Паскале применяются так называемые типизированные указатели — переменные, хранящие адрес, относительно которого точно известно, переменная какого типа расположена в соответствующей области памяти. Для обозначения указателя в оригинальном виртовском описании Паскаля использовался символ “↑”, но в ASCII (а равно и на вашей клавиатуре) такого символа нет, поэтому во всех реально существующих версиях Паскаля используется символ “ˆ” (вы легко найдёте эту “крышку” на клавише “6”). Например, если описать две переменные

то р сможет хранить адрес переменной, имеющей тип integer, a q сможет хранить адрес переменной, имеющей тип real.

Адрес переменной можно получить с помощью операции взятия адреса, которая обозначается знаком “@”³⁹, то есть, например, выражение @х даёт адрес переменной х. В частности, если описать переменную типа real и переменную типа указатель на real:

то станет возможно занести адрес первой переменной во вторую:

Указатели и вообще адресные выражения были бы совершенно бесполезны, если бы нельзя было что-то сделать с областью памяти (т.е., в большинстве случаев, с переменной), зная только её адрес. Для этого в Паскале используется операция dereference, название которой на русский язык часто переводится неказистым словом “разыменование”, хотя можно было бы использовать, например, термин “обращение по адресу”. Обозначается эта операция уже знакомым нам символом “ˆ”, который ставится после имени указателя (или, говоря в общем, после произвольного адресного выражения, в качестве которого может выступать, например, вызов функции, возвращающей адрес). Так, после присваивания адреса из вышеприведённого примера выражение рˆ будет обозначать “то, на что указывает р”, то есть в данном случае переменную г. В частности, оператор

занесёт в память, находящуюся по адресу, хранящемуся в р (то есть попросту в переменную r) значение 25.7, а оператор

напечатает это значение.

Отметим ещё один важный момент. В Паскале предусмотрены также нетипизированные указатели (и адреса), для которых введён встроенный тип pointer. Адреса этого типа компилятор рассматривает просто как абстрактные адреса ячеек памяти, не делая никаких предположений о том, значения какого типа находятся в памяти по такому адресу; указатели этого типа, соответственно, способны хранить произвольный адрес в памяти вне зависимости от того, что там, по этому адресу, находится. Если мы опишем переменную типа pointer, например

то в такую переменную можно будет занести адрес любого типа; мало того, значение этой переменной можно будет присвоить переменной любого указательного типа, что вообще-то чревато ошибками: к примеру, можно занести в ар адрес какой-нибудь переменной типа string, а потом забыть про это и присвоить её значение переменной типа “integer; если теперь попробовать с такой переменной работать, ничего хорошего не выйдет, ведь на самом деле по этому адресу находится не integer, a string. Следует поэтому соблюдать крайнюю осторожность при работе с нетипизированными указателями, а лучше не использовать их вовсе, пока это всерьёз не потребуется. Отметим, что такая потребность возникнет у вас не скоро, если вообще возникнет: реальная необходимость в применении нетипизированных указателей появляется при создании нетривиальных структур данных, какие могут понадобиться только в больших и сложных программах.

Мы могли бы вообще не упоминать нетипизированные указатели в нашей книге, если бы не то обстоятельство, что результатом операции взятия адреса является как раз нетипизированный адрес. Почему создатели Turbo Pascal, впервые внедрившие операцию взятия адреса в этот язык, поступили именно так — остаётся непонятным (например, в языке Си точно такая же операция прекрасно справляется с формированием типизированного адреса).

Есть и ещё один важный случай нетипизированного адресного выражения — встроенная константа nil. Она обозначает недействительный адрес, то есть такой, по которому в памяти заведомо не может находиться ни одна переменная, и присваивается переменным указательных типов, чтобы показать, что данный указатель сейчас никуда не указывает. Константу nil иногда называют нулевым указателем.

Если попытаться выделить из этого параграфа “сухой остаток”, мы получим следующее:

• если t — это некий тип, то ˆt — это тип “указатель на t”;

• если х — произвольная переменная, то выражение @х означает “адрес переменной х” (причём нетипизированный);

• если р — это указатель (или другое адресное выражение), то рˆ обозначает “то, на что указывает р”;

• словом nil обозначается специальный “нулевой адрес”, используемый, чтобы показать, что данный указатель сейчас ни на что не указывает.

2.13.3. Динамические переменные

Как мы уже отмечали, под динамической переменной понимается такая переменная (т. е. область памяти), которая создаётся во время выполнения программы. Ясно, что у такой переменной не может быть имени, ведь все имена мы задаём, когда пишем программу. Работа с динамическими переменными производится с использованием их адресов, хранящихся в указателях.

Память под динамические переменные выделяется из специальной области памяти, которую называют кучей (англ. heap). При уничтожении динамической переменной память возвращается обратно в “кучу” и может быть выделена под другую динамическую переменную. Если в куче не хватает места, наша программа (незаметно для нас) обращается к операционной системе с просьбой выдать больше памяти, за счёт чего увеличивает размер кучи. Следует учитывать, что уменьшить размер кучи невозможно, то есть если наша программа уже затребовала и получила память от операционной системы, то эта память останется в распоряжении программы до её завершения. Из этого, например, следует, что если вам надо одномоментно создать какую-то динамическую переменную, а какую-то другую уничтожить, то лучше сначала уничтожить старую переменную, а потом создавать новую. Иногда это позволяет сэкономить на общем размере кучи.

Создание динамической переменной производится с помощью псевдопроцедуры new, которая должна быть применена к типизированному указателю. При этом происходят две вещи: во-первых, из кучи выделяется область памяти нужного размера, в которой будет теперь размещаться свежесозданная динамическая переменная (собственно, эта динамическая переменная и есть та область памяти, которую только что выделили); во-вторых, в заданный указатель заносится адрес созданной динамической переменной.

Например, если мы описали указатель

то теперь мы можем создать динамическую переменную типа string; делается это с помощью new:

При выполнении этого new, во-первых, из кучи будет выделена область памяти размером в 256 байт, которая как раз и станет нашей новой (динамической) переменной типа string; во-вторых, в переменную р будет занесён адрес этой области памяти. Таким образом, у нас теперь есть безымянная переменная типа string, единственный способ доступа к которой — через её адрес: выражение рˆ как раз соответствует этой переменной. Мы можем, к примеру, занести в эту переменную значение:

Полученная в памяти программы структура может быть схематически представлена как показано на рис. 2.4.

Рис. 2.4. Указатель на строку в динамической памяти

Удаление динамической переменной, которая нам больше не нужна, производится с помощью псевдопроцедуры dispose; параметром ей служит адрес переменной, которую нужно ликвидировать:

При этом, как ни странно, значение указателя р не меняется; единственное, что происходит — это возвращение памяти, которая была занята под переменную рˆ, обратно в кучу; иначе говоря, меняется статус этой области памяти, вместо занятой она помечается как свободная и доступная к выдаче по требованию (одним из следующих new). Конечно, использовать значение указателя р после этого нельзя, ведь мы сами сообщили менеджеру кучи, что более не собираемся работать с переменной рˆ.

Важно понимать, что динамическая переменная не привязана к конкретному указателю. Например, если у нас есть два указателя:

то мы можем выделить память, используя один из них:

потом в какой-то момент занести этот адрес в другой указатель:

и работать с полученной переменной, обозначая её как с qˆ вместо рˆ; в самом деле, ведь адрес нашей переменной теперь есть в обоих указателях. Более того, мы можем занять указатель р под что-то другое, а работу с ранее выделенной переменной проводить только через q, и, когда придёт время, удалить эту переменную, используя, опять же, указатель q:

Важен здесь сам адрес (т. е. значение адреса), а не то, в каком из указателей этот адрес нынче лежит.

Ещё один крайне важный момент состоит в том, что при определённой небрежности можно легко потерять адрес динамической переменной. Например, если мы создадим переменную с помощью new(p), поработаем с ней, а потом, не удалив эту переменную, снова выполним new(p), то менеджер кучи выделит нам новую переменную и занесёт её адрес в указатель р; как всегда в таких случаях, старое значение переменной р будет потеряно, но ведь там хранился адрес первой выделенной динамической переменной, а к ней у нас нет больше никаких способов доступа!

Динамическая переменная, которую забыли освободить, но на которую больше не указывает ни один указатель, становится так называемым мусором (англ. garbage; не следует путать этот термин со словом junk, которое тоже переводится как мусор, но в программировании обычно обозначает бессмысленные данные, а не потерянную память). В некоторых языках программирования предусмотрена так называемая сборка мусора, которая обеспечивает автоматическое обнаружение таких переменных и их возвращение в кучу, но в Паскале такого нет, и это, в целом, даже хорошо. Дело в том, что механизмы сборки мусора довольно сложны и зачастую срабатывают в самый неподходящий момент, “подвешивая” на некоторое время выполнение нашей программы; например, на соревнованиях автомобилей-роботов DARPA Grand Challenge в 2005 году одна из машин, находившаяся под управлением ОС Linux и программ на языке Java, влетела на скорости около 100 км/ч в бетонную стену, причём в качестве одной из возможных причин специалисты назвали не вовремя включившийся сборщик мусора.

Так или иначе, в Паскале сборка мусора не предусмотрена, так что нам необходимо внимательно следить за удалением ненужных динамических переменных; в противном случае мы можем очень быстро исчерпать доступную память.

Кстати, процесс образования мусора программисты называют утечкой памяти (англ. memory leaks). Отметим, что утечка памяти свидетельствует только об одном: о безалаберности и невнимательности автора программы. Никаких оправданий утечке памяти быть не может, и если вам кто-то попытается заявить противоположное, не верьте: такой человек просто не умеет программировать.

От материала этого параграфа может остаться некоторое недоумение. В самом деле, зачем описывать указатель (например, на строку, как в нашем примере), а потом делать какой-то там new, если можно сразу описать переменную типа string и работать с ней как обычно?

Некоторый смысл работа с динамическими переменными получает, если эти переменные имеют сравнительно большой размер, например, в несколько сот килобайт (это может быть какой-нибудь массив записей, некоторые поля которых тоже являются массивами, и т. п.); описывать переменную такого размера в качестве обычной локальной попросту опасно, может не хватить стековой памяти, а вот с размещением её же в куче никаких проблем не возникнет; кроме того, если у вас много таких переменных, но не все они нужны одновременно, может оказаться полезным создавать и удалять их по мере необходимости. Однако все эти примеры, откровенно говоря, притянуты за уши; указатели почти никогда не используются таким образом. В полной мере возможности указателей раскрываются только при создании так называемых связных динамических структур данных, которые состоят из отдельных переменных типа “запись”, причём каждая такая переменная содержит один или несколько указателей на другие переменные того же типа. Некоторые из таких структур данных мы рассмотрим в следующих параграфах.

2.13.4. Односвязные списки

Пожалуй, самой простой динамической структурой данных оказывается так называемый односвязный список. Такой список строится из звеньев, каждое из которых, представляя собой переменную типа “запись”, в качестве одного из своих полей имеет указатель на следующий элемент списка; очевидно, что такое поле должно иметь тип “указатель на запись того же типа”. Последний элемент списка содержит в этом поле значение nil, чтобы показать, что больше элементов нет. Достаточно при этом в каком-нибудь указателе хранить адрес самого первого элемента списка, и мы сможем при необходимости добраться до любого другого его элемента.

Слово “односвязный” в названии этой структуры данных означает, что на каждый из его элементов указывает один указатель; впрочем, с тем же успехом можно отметить, что каждый элемент имеет одно поле, предназначенное для сохранения связности списка, и заявить, что “односвязность” предполагает именно это. Наконец, можно сказать, что в списке выстроена одна цепочка связей из указателей и списать загадочную “односвязность” на этот факт. Как мы увидим позже, все эти утверждения эквивалентны.

Пример односвязного списка из трёх элементов, содержащих целые числа 25, 36 и 49, показан на рис. 2.5. Для создания такого списка нам потребуется запись, состоящая из двух полей: первое будет хранить целое число, второе — адрес следующего звена списка. Здесь в Паскале имеется некая хитрость: использовать имя описываемого типа при описании его собственных полей почему-то нельзя, то есть мы не можем написать вот так:

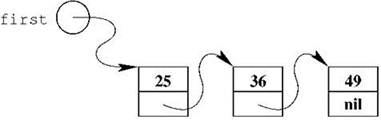
Рис. 2.5. Односвязный список из трёх элементов

При этом Паскаль позволяет описать указательный тип, используя такое имя типа, которое пока ещё не введено; как следствие, мы можем дать отдельное имя типу указателя на item до того, как опишем сам тип item, а при описании item воспользоваться этим именем, например:

Такое описание никаких возражений у компилятора не вызовет. Имея типы item и itemptr, мы можем описать указатель для работы со списком:

ну а сам список, показанный на рисунке, можно создать, например, так:

С непривычки конструкции вроде firstˆ.nextˆ.data могут напугать; это вполне нормальная реакция, но позволить себе долго бояться мы не можем, поэтому нам придётся тщательно разобраться, что тут происходит. Итак, коль скоро у нас указатель на первый элемент называется first, то выражение firstˆ будет обозначать весь этот элемент целиком. Поскольку сам этот элемент представляет собой запись из двух полей, доступ к полям, как и для любой записи, производится через точку и имя поля; таким образом, firstˆ.data — это поле первого элемента, в котором содержится целое число (на рисунке и в нашем примере это число 25), a firstˆ.next — это указатель на следующий (второй) элемент списка. В свою очередь, firstˆ.nextˆ — это сам второй элемент списка, и так далее (см. рис. 2.6).

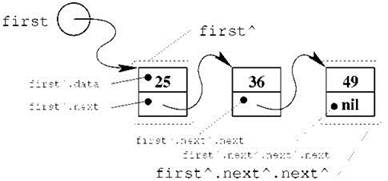
Рис. 2.6. Навигация в односвязном списке

Если что-то здесь осталось непонятно, двигаться дальше нет никакого смысла! Сначала добейтесь понимания происходящего, в противном случае в дальнейшем тексте вы тем более ничего не поймёте.

Конечно, в большинстве случаев со списками работают совсем не так; пример, потребовавший устрашающего выражения firstˆ.nextˆ.nextˆ.next, мы привели скорее для иллюстрации. Гораздо чаще при работе с односвязным списком поступают одним из двух способов: либо заносят элементы всегда в его начало (это делается с помощью вспомогательного указателя), либо хранят два указателя — на начало и конец списка, а элементы заносят всегда в конец. Прежде чем показать, как это делается, мы предложим вашему вниманию две задачи, которые настоятельно рекомендуется хотя бы попробовать решить самостоятельно, причём до того, как вы прочитаете остаток этого параграфа. Дело в том, что, самостоятельно догадавшись, как это делается, вы уже никогда этого не забудете, и работа со списками никогда больше не вызовет у вас проблем; если же вы сразу начнёте с разбора примеров, которые мы приведём дальше, то понять, как всё это делать самостоятельно, окажется гораздо сложнее, потому что побороть искушение писать “по аналогии” (то есть без достижения полного понимания происходящего) часто не могут даже самые волевые люди.

Итак, вот первая задача; она потребует создания односвязного списка и добавления элементов в его начало:

Написать программу, которая читает целые числа из потока стандартного ввода до возникновения ситуации “конец файла”, после чего печатает все введённые числа в обратном порядке. Количество чисел заранее неизвестно, вводить явные ограничения на это количество запрещается.

Вторая задача также потребует использования односвязного списка, но добавлять новые элементы придётся в его конец, для чего нужно будет работать со списком через два указателя: первый будет хранить адрес первого элемента списка, второй — адрес последнего элемента.

Написать программу, которая читает целые числа из потока стандартного ввода до возникновения ситуации ““конец файла”, после чего дважды печатает все введённые числа в том порядке, в котором они были введены. Количество чисел заранее неизвестно, вводить явные ограничения на это количество запрещается.

Учтите, что считать подобного рода задачи решёнными можно не раньше, чем у вас на компьютере заработает (причём заработает правильно) написанная вами программа, соответствующая условиям. Даже в этом случае задача не всегда оказывается верно решённой, поскольку вы можете упустить при её тестировании какие-то важные случаи или просто неверно истолковать получаемые результаты; но если работающей программы вообще нет, то о том, что задача решена, заведомо не может быть никакой речи.

В надежде, что вы как минимум попробовали решить предложенные задачи, мы продолжим обсуждение работы со списками. Прежде всего отметим один крайне важный момент. Если контекст решаемой задачи предполагает, что вы начинаете работу с пустого списка, то есть со списка, не содержащего ни одного элемента, обязательно превратите ваш указатель в корректный пустой список, занеся в него значение nil. Начинающие часто забывают про это, получая на выходе постоянные аварии.

Добавление элемента в начало односвязного списка производится в три этапа. Сначала, используя вспомогательный указатель, мы создаём (в динамической памяти) новый элемент списка. Затем мы заполняем этот элемент; в частности, мы делаем так, чтобы его указатель на следующий элемент стал указывать на тот элемент списка, который сейчас (пока) является первым, а после добавления нового станет вторым, т. е. как раз следующим после нового. Нужный адрес, как несложно догадаться, находится в указателе на первый элемент списка, его-то мы и присвоим полю next в новом элементе. Наконец, третий шаг — признать новый элемент новым первым элементом списка; это делается занесением его адреса в указатель, хранящий адрес первого элемента.

Схематически происходящее показано на рис. 2.7 на примере всё того же списка целых чисел, состоящего из элементов типа item, причём адрес первого элемента списка хранится в указателе first; сначала в этом списке находятся элементы, хранящие числа 36 и 49 (рис. 2.7, “а)”), и нам нужно занести в его начало новый элемент, содержащий число 25. Для этого мы вводим дополнительный указатель, который будет называться tmp от английского temporary, что означает “временный”:

На первом шаге мы, как уже было сказано, создаём новый элемент:

Получившаяся после этого ситуация показана на рис. 2.7, “b)”. Со списком ещё ничего не произошло, созданный новый элемент никак его не затрагивает. Сам элемент пока остаётся сильно “недоделанным”: в обоих его полях находится непонятный мусор, что показано на рисунке символом “?!”. Пора делать второй шаг — заполнять поля нового элемента. В поле data нам нужно будет занести искомое число 25, тогда как поле next должно указывать на тот элемент, который (после включения нового элемента в список) станет следующим после нового; это, собственно, тот элемент, который сейчас пока в списке первый, то есть его адрес хранится в указателе first, его-то мы и присвоим полю next:

Состояние нашей структуры данных после этих присваиваний показано на рис. 2.7, “с)”. Осталось лишь финальным ударом объявить новый (и полностью подготовленный к своей роли) элемент первым элементом списка, присвоив его адрес указателю first; поскольку этот адрес хранится в tmp, всё оказывается совсем просто:

Финальная ситуация показана на рис. 2.7, “d)”. Забыв про наш временный указатель и про то, что первый элемент списка только что был “новым”, мы получаем ровно то состояние списка, к которому стремились.

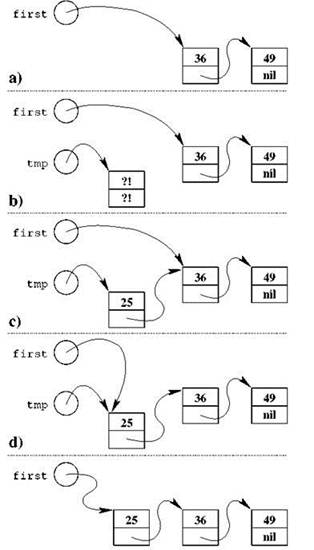
Рис. 2.7. Занесение нового элемента в начало односвязного списка

С этой трёхшаговой процедурой добавления нового элемента в начало связано одно замечательное свойство: для случая пустого списка последовательность действий по добавлению первого элемента полностью совпадает с последовательностью действий по добавлению нового элемента в начало списка, уже содержащего элементы. Соответствующая последовательность состояний структуры данных показана на рис. 2.8: вначале список пуст (“а)”); на первом шаге мы создаём новый элемент (“b)”); на втором шаге заполняем его (“с)”); последним действием делаем этот новый элемент первым элементом списка (“d)”). Всё это работает только при условии, что мы не забыли перед началом работы со списком сделать его корректным, занеся значение nil в указатель first!

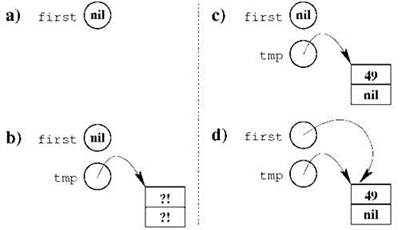
Рис. 2.8. Работа процедуры занесения в начало при исходно пустом списке

Если всё время заносить элементы в начало списка, то располагаться в списке они будут в порядке, противоположном тому, в котором их туда заносили; именно это и требуется в первой из двух предложенных ранее задач. Решение будет состоять из двух циклов, в первом из них будет выполняться чтение чисел до тех пор, пока не настанет ситуация “конец файла”⁴⁰, и после прочтения очередного числа оно будет добавляться в начало списка; после этого останется только пройти по списку из его начала до конца, печатая содержащиеся в нём числа. Программа целиком будет выглядеть так:

В этом тексте мы ни разу не использовали dispose; здесь высвобождение памяти не имеет большого смысла, поскольку сразу после первого (и единственного) использования построенного списка программа завершается, так что вся память, отведённая ей в системе, освобождается; разумеется, это касается в том числе и кучи. В более сложных программах, например, таких, которые строят один список за другим и так много раз, забывать про освобождение памяти ни в коем случае нельзя. Освободить память от односвязного списка можно с помощью цикла, в котором на каждом шаге из списка удаляется первый элемент, и так до тех пор, пока список не опустеет. При этом тоже есть своя хитрость. Если просто взять и сделать dispose(first), первый элемент списка перестанет существовать, а значит, мы уже не сможем использовать его поля, но ведь адрес второго элемента хранится именно там. Поэтому прежде чем уничтожать первый элемент, необходимо запомнить адрес следующего; после этого первый элемент уничтожается, а указателю first присваивается адрес следующего элемента, сохранённый во вспомогательном указателе. Соответствующий цикл выглядит так:

Можно поступить и иначе: запомнив адрес первого элемента во вспомогательном указателе, исключить этот элемент из списка, соответствующим образом изменив first, и уже после этого удалить его:

На рис. 2.9 первый способ показан слева, второй — справа. Какой из них лучше, можете решить для себя сами; по эффективности между ними никакой разницы нет.

Рис. 2.9. Два способа удаления первого элемента из односвязного списка

Как можно заметить, условие второй из предложенных раньше задач от условия первой отличается в основном порядком выдачи элементов на печать. В принципе, никто не мешает построить список, как и для первой задачи, “задом наперёд”, а потом отдельным циклом “перевернуть” его (как это сделать, попробуйте придумать сами в качестве упражнения); но правильнее будет всё же сразу построить список в нужном порядке, для чего нам потребуется добавление элементов в конец списка, а не в его начало.

Если односвязный список предполагается увеличивать “с конца”, обычно для этого хранят не один указатель, как в предшествующих примерах, а два: на первый элемент списка и на последний. Когда список пуст, оба указателя должны иметь значение nil. Процедура занесения нового элемента в такой список (в его конец) выглядит даже проще, чем только что рассмотренная процедура занесения в начало: если, к примеру, указатель на последний элемент называется last, то мы можем создать новый элемент сразу где надо, то есть занести его адрес в lastˆ.next, затем сдвинуть указатель last на новоиспечённый последний элемент и уже после этого заполнить его поля; если нам нужно занести в список число 49, это можно сделать так (см. рис. 2.10):

Как это часто случается, всякое упрощение имеет свою цену. В отличие от занесения в начало, когда для списка хранится только указатель first, при наличии двух указателей занесение первого элемента оказывается специальным случаем, который требует совершенно иного набора действий: в самом деле, указатель last в этой ситуации никуда не указывает, ведь последнего элемента пока не существует (и вообще никакого не существует), так что не существует и переменной lastˆ.next, которую мы столь лихо задействовали. Правильная последовательность действий для занесения числа 49 в этом случае будет такая:

Как видим, последние две строки остались точно такими же, как и раньше (мы специально постарались так сделать), тогда как первые две совершенно поменялись. Сказанное можно обобщить. Если число, которое мы заносим в список, находится в переменной n, причём мы не знаем, есть к этому времени в списке хотя бы один элемент или нет, то корректный код для занесения элемента в список будет таким:

Полностью решение второй задачи мы не приводим; с учётом всего сказанного оно должно быть совершенно очевидно.

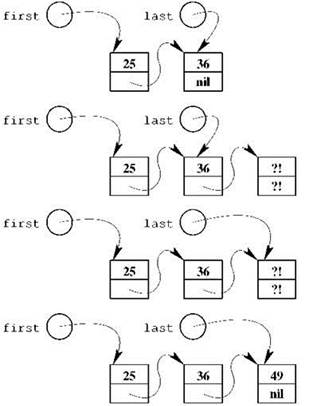
Рис. 2.10. Добавление нового элемента в конец списка

2.13.5. Стек и очередь

В некоторых учебниках по информатике можно встретить утверждение, что-де “стек” и “очередь” — это такие структуры данных; стеком в таких случаях обычно называют ту сущность, которую мы в предыдущем параграфе называли односвязным списком. Нам остаётся лишь призвать читателя не верить в подобные антинаучные россказни; на самом деле как стек, так и очередь могут быть реализованы совершенно разными структурами данных (списками, массивами, разнообразными комбинациями того и другого, ту же очередь часто реализуют с помощью кольцевого буфера и т. д.; больше того, значения даже не обязательно хранить в оперативной памяти, часто приходится использовать файлы на диске); сами по себе стек и очередь определяются не тем, какова реализующая их структура данных, а тем, каковы доступные пользователю операции и как эти операции работают.

Как стек, так и очередь представляют собой некий абстрактный “объект”, обеспечивающий (неважно как) хранение значений определённого типа, причём для этого объекта определены две базовые операции: добавление нового значения и извлечение значения. Разница в том, в каком порядке происходит извлечение: из очереди значения извлекаются в том же порядке, в каком их туда занесли, а из стека — в обратном. По-английски очередь обычно обозначают аббревиатурой FIFO (first in, first out, т. е. “первым вошёл — первым вышел”), а стеки — аббревиатурой LIFO (last in, first out, “последним вошёл — первым вышел”).

Иначе говоря, очередь — это такая штука, куда можно складывать значения какого-нибудь типа (например, целочисленного), а можно их оттуда извлекать, и при извлечении мы всегда получаем значение, которое (среди тех, что были занесены, но пока что не были извлечены) в нашей очереди пролежало дольше других; со стеком ситуация обратная: первыми извлекаются самые “свежие” значения.

Самый простой вариант реализации стека нам уже известен: это односвязный список, при работе с которым мы всегда имеем дело с его началом: именно в начало добавляются новые элементы, и извлекаются элементы тоже из начала. Немного подумав, мы можем заметить, что очередь тоже очень легко реализовать на базе односвязного списка, только добавление новых элементов следует производить не в начало, а в конец (а извлекать элементы по-прежнему из начала).

Обратим внимание, что речь в обоих случаях идёт о реализации механизма, относительно которого нам важны доступные операции, а то, как эти операции сделаны, может остаться за кадром. Такая ситуация в программировании возникает достаточно часто; именно этот факт породил так называемое объектно-ориентированное программирование, суперпопулярное в наше время. Что это такое, мы узнаем позже; в третьем томе нашей книги этому будет посвящена отдельная часть. Пока до ООП дело не дошло, отметим, что в любой подобной ситуации программисты стараются создать набор подпрограмм (процедур), реализующих все нужные операции, причём описать их так, чтобы даже в случае изменения принципов реализации (в нашем случае, например, при переходе от использования списка к использованию какого-нибудь массива) поменялся только текст этих процедур, а программист, использующий их, вообще ничего не заметил.

Иначе говоря, если кто-то просит нас реализовать тот же стек или какой-то другой абстрактный объект, для которого важны операции, а не его внутреннее устройство, мы обычно пишем набор процедур и функций и объясняем, как этим набором пользоваться, при этом тщательно следим, чтобы все наши объяснения никак не зависели от того, что мы используем внутри наших процедур в качестве механизма реализации. Такой набор процедур вместе с пояснениями, как их нужно использовать, называется интерфейсом⁴¹. Считается, что интерфейс придуман удачно, если никакие изменения в деталях реализации нашего абстрактного объекта не приводят к изменениям ни в самом интерфейсе, ни в объяснениях, как им пользоваться, то есть могут безболезненно игнорироваться теми программистами, которые станут использовать наше изделие.

Один из подходов, позволяющих создавать хорошие интерфейсы, состоит в том, чтобы сначала придумать именно интерфейс, исходя из набора операций, которых от нас ожидает пользователь, и уже потом попытаться написать какую-то реализацию, которая позволит процедурам нашего интерфейса работать в соответствии с замыслом. Поскольку о реализации мы начинаем думать уже после создания интерфейса, такой интерфейс с хорошей вероятностью окажется не зависящим от конкретной реализации, что нам и требуется.

Попробуем применить сказанное к случаю стека; для определённости пусть это будет стек целых чисел типа longint. Ясно, что, какова бы ни была его реализация, хоть что-то, хоть какую-то информацию нам при этом обязательно придётся хранить (при реализации в виде односвязного списка это будет указатель на первый элемент списка, но мы пока об этом думать не хотим). Хранить информацию мы можем только в переменных, причём если мы вспомним о существовании переменных типа “запись”, то заметим, что любую информацию (разумного размера) мы можем при желании сохранить в одной переменной, нужно только выбрать для неё подходящий тип. Итак, какова бы ни была реализация нашего стека, нам необходимо и достаточно для каждого вводимого стека (которых может быть сколько угодно) описать переменную некоего типа; не зная, какова будет реализация, мы не можем сказать, какой конкретно это будет тип, но это не помешает нам дать ему имя. Поскольку речь идёт о стеке чисел типа longint, назовём этот тип StackOfLongints.

Основные операции над стеком по традиции обозначаются словами push (добавление значения в стек) и pop (извлечение значения). Обе эти операции мы реализуем в виде подпрограмм; в принципе, было бы логично соответствующие подпрограммы назвать как-то вроде StackOfLongintsPush и StackOfLongintsPop, но, посмотрев внимательно на получившиеся длинные имена, мы можем (вполне естественно) усомниться в том, что пользоваться ими будет удобно. Поэтому везде, кроме собственно имени типа, мы громоздкое StackOfLongints заменим на короткое SOL, а подпрограммы назовём, соответственно, SOLPush и SOLPop. Заметим ещё, что занесение нового элемента в стек всегда проходит удачно⁴², тогда как извлечение из стека, если он пуст, успешным считаться не может. Поэтому SOLPush у нас будет процедурой, получающей на вход два параметра — сам стек и число, которое в него нужно занести (причём стек будет передаваться как параметр-переменная, а число — как простой параметр), тогда как SOLPop будет оформлена в виде логической функции, возвращающей истину в случае успеха и ложь при неудаче; параметров у неё тоже будет два — переменная-стек и переменная типа longint, в которую (в случае успеха) будет записываться результат.

Собственно говоря, мы почти закончили придумывать интерфейс. Добавим для удобства ещё функцию SOLIsEmpty, получающую в качестве параметра стек и возвращающую истину, если он пуст, и ложь в противном случае. Наконец, вспомним, что переменная может, если ей ничего не присвоить, содержать произвольный мусор, и добавим процедуру, превращающую свежеописанную переменную в корректный пустой стек; назовём её SOLInit. Всё, интерфейс готов. Вспомнив наш подход к пошаговой детализации, при котором для начала пишутся пустые подпрограммы, мы можем зафиксировать наш интерфейс в виде фрагмента программы:

Конечно, такой фрагмент даже не откомпилируется, поскольку мы не указали, что такое StackOfLongints; но ведь надо же с чего-то начинать. Теперь, когда интерфейс полностью зафиксирован, мы можем приступить к реализации. Поскольку мы хотели использовать односвязный список, нам потребуется тип для его звена:

Теперь мы можем начать обращивать “мясом” наши “заглушки” интерфейсных подпрограмм. Для начала заметим, что для работы со стеком нужен только указатель на начало списка, так что в качестве переменной типа StackOfLongints можно использовать переменную типа LongItemPtr. Отразим этот факт:

Теперь берём наши четыре подпрограммы и реализуем их тела:

С использованием этих процедур решение задачи о выдаче введённой последовательности чисел в обратном порядке, которую мы рассматривали в предыдущем параграфе, может стать гораздо изящнее:

Второй цикл можно записать ещё короче:

Попробуем применить ту же методику к очереди. Ясно, что какая-то переменная нам для организации очереди точно понадобится; назовём её тип QueueOfLongints. Основные операции над очередью, в отличие от стека, обычно называют put и get; как и для стека, для очереди будут нужны процедура инициализации и функция, позволяющая узнать, не пуста ли очередь. Для фиксации интерфейса можно написать следующие заглушки:

Для реализации используем список из элементов того же типа LongItem, но заметим, что нам нужно для представления очереди два указателя типа LongItemPtr; чтобы объединить их в одну переменную, воспользуемся записью:

Реализация интерфейсных процедур будет выглядеть так:

2.13.6. Проход no списку указателем на указатель

Рассмотрим довольно простую задачу: пусть у нас есть всё тот же список целых чисел и нам нужно удалить из него все элементы, содержащие отрицательные значения. Сложность здесь в том, что для удаления элемента из списка необходимо изменить тот указатель, который на него указывает; если удаляемый элемент в списке не первый, то изменять нужно значение указателя nextв предыдущем элементе списка, если же он первый, то изменять нужно указатель first.

Сходу становится ясно, что выполнять проход по списку так, как мы это делали, например, для его печати, в этой задаче не получится. В самом деле, выполняя цикл по знакомой нам схеме

мы на момент работы с элементом уже не помним, где находится в памяти предыдущий элемент, и не можем изменить значение его поля next. Можно попытаться с этой проблемой справиться, храня в переменной цикла как раз адрес предыдущего элемента:

но тогда первый элемент списка придётся обрабатывать отдельно; это, в свою очередь, повлечёт специальную обработку для случая пустого списка. В итоге для удаления всех отрицательных значений мы получим что-то вроде следующего фрагмента:

Полученное решение трудно назвать красивым: фрагмент получился громоздким из-за наличия двух циклов и объемлющего if’а, его достаточно трудно читать. Между тем, на самом деле при удалении первого элемента и любого другого действия выполняются абсолютно одинаковые, только в первом случае они выполняются над указателем first, а во втором — над tmpˆ.next.

Сократить размеры и сделать решение понятнее позволяет нетривиальный приём, предполагающий задействование указателя на указатель. Если тип звена списка у нас называется, как и раньше, item, а тип указателя на него — itemptr, то такой указатель на указатель описывается следующим образом:

Полученная переменная pp может содержать адрес указателя на item, то есть она с одинаковым успехом может хранить в себе как адрес нашего first, так и адрес поля next, расположенного в любом из элементов списка. Именно этого мы и добиваемся; цикл прохода по списку с удалением отрицательных элементов мы организуем с помощью pp в качестве переменной цикла, причём в pp сначала будет содержаться адрес first, затем — адрес next из первого звена списка, из второго звена и так далее (см. рис. 2.11). В целом рр будет в каждый момент времени указывать на указатель, в котором располагается адрес текущего (рассматриваемого) звена списка. Начальное значение переменная рр получит в результате очевидного присваивания рр := @first, переход к рассмотрению следующего элемента будет выглядеть несколько сложнее:

Если две “крышки” после рр кажутся вам чем-то слишком сложным, вспомните, что ррˆ есть то, на что указывает рр, то есть, как мы договорились, указатель на текущий элемент; следовательно, ррˆˆ есть сам этот текущий элемент, ррˆˆ.next — это его поле next (то есть как раз указатель на следующий элемент), от него мы берём адрес, этот адрес заносим в рр — и после этого мы готовы к работе со следующим элементом.

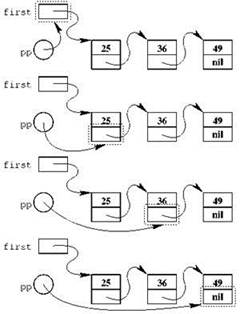
Рис. 2.11. Указатель на указатель в качестве переменной цикла

Отметим, что переход к следующему следует выполнять только в том случае, если текущий элемент мы не удалили; если же элемент был удалён, то переход к рассмотрению следующего за ним произойдёт сам собой, ведь хотя адрес в рр у нас не изменится, но изменится адрес, хранящийся в указателе ррˆ (будь то first или очередное поле next, неважно).

Осталось понять, каково должно быть условие такого цикла. Закончить работу следует, когда очередного элемента нет, то есть когда указатель на очередной элемент содержит nil. Это опять-таки может оказаться как указатель first (если список пуст), так и поле next последнего элемента в списке (если в нём есть хотя бы один элемент). Проверить такое условие можно выражением ррˆ<> nil. Окончательно (в предположении, что переменная tmр имеет, как и раньше, тип itеmрtr, а переменная рр имеет тип ˆitemрtr) наш цикл примет следующий вид:

Сравнивая это решение с предыдущим, можно заметить, что оно практически дословно повторяет цикл, который в том решении был внутренним, но при этом у нас исчез объемлющий if и отдельный цикл для удаления элементов из начала. Применение указателя на указатель позволило нам обобщить основной цикл, сняв тем самым необходимость в обработке особых случаев.

Применение указателя на указатель позволяет не только удалять элементы из произвольного места списка, но и вставлять элементы в любую его позицию — точнее, в то место, куда сейчас указывает указатель, на который указывает рабочий указатель. Если в рабочем указателе находится адрес указателя first, вставка будет выполняться в начало списка, если же там адрес поля next одного из звеньев списка, то вставка произойдёт после этого звена, т. е. перед следующим звеном. Это может оказаться и вставка в конец списка, если только в рабочем указателе будет находиться адрес поля next из последнего звена списка. Например, если рабочий указатель у нас по-прежнему называется рр, вспомогательный указатель типа itemptr называется tmp, а число, которое нужно добавить в список, хранится в переменной n, то вставка звена с числом n в позицию, обозначенную с помощью рр, будет выглядеть так:

Как можно заметить, этот фрагмент дословно повторяет процедуру вставки элемента в начало односвязного списка, которую мы рассматривали на стр. 360, только вместо first используется ррˆ; как и в случае с удалением элемента, такой способ вставки элемента представляет собой обобщение процедуры вставки в начало. Обобщение основано на том, что любой “хвост” односвязного списка также представляет собой односвязный список, только вместо first для него используется поле next из элемента, предшествующего такому “хвосту”. Этим фактом мы ещё воспользуемся; помимо прочего, он позволяет довольно естественное применение рекурсии для обработки односвязных списков.

Умея вставлять звенья в произвольные места списка, мы можем, например, работать со списком чисел, отсортированных по возрастанию (или по убыванию, или по любому другому критерию). При этом нужно следить за тем, чтобы каждый элемент вставлялся точно в нужную позицию списка — так, чтобы после такого добавления список оставался отсортированным.

Делается это достаточно просто. Если, как и раньше, число, которое нужно вставить, хранится в переменной n, а список, на начало которого указывает first, при этом отсортирован в порядке возрастания, то вставка нового элемента быть сделана, например, так:

Интерес здесь представляют только первые три строчки, остальные четыре мы уже видели. Цикл while здесь позволяет найти нужное место в списке, или, точнее, тот указатель, который указывает на звено, перед которым надо вставить новый элемент. Начинаем мы, как обычно, с начала, в данном случае это означает, что в рабочий указатель заносится адрес указателя first. Очередного элемента в списке может вообще не оказаться — если в списке нет вообще ни одного элемента, либо если все значения, хранящиеся в списке, оказались меньше того, которое будет вставлено сейчас; при этом в указателе ррˆ (то есть в том, на который указывает наш рабочий указатель) окажется значение nil — отсюда первая часть условия в цикле. В такой ситуации идти нам дальше некуда, вставлять нужно прямо сейчас.

Вторая часть условия цикла обеспечивает поиск нужной позиции: пока очередной элемент списка меньше, чем вставляемый, нам нужно двигаться по списку дальше.

Здесь можно обратить внимание на одну важную особенность вычисления логических выражений. Если, к примеру, указатель ррˆ оказался равен nil, то попытка обратиться к переменной ррˆˆ.data приведёт к немедленному аварийному завершению программы, ведь записи ррˆˆ попросту не существует. К счастью, такого обращения не произойдёт. Так получается, потому что при вычислении логических выражений Free Pascal использует “ленивую семантику”: если значение выражения уже известно, дальнейшие его подвыражения не вычисляются. В данном случае между двумя частями условия стоит связка and, так что, если первая часть ложна, то к всё выражение окажется ложным, поэтому вычислять его вторую часть не нужно.

Полезно будет знать, что в оригинальном Паскале, как его описал Никлаус Вирт, этого свойства не было: при вычислении любого выражения там обязательно вычислялись все его подвыражения. Если бы Free Pascal в этом плане действовал так же, нам пришлось бы изрядно покрутиться, поскольку вычисление условия (ррˆ <> nil) and (ррˆˆ.data < n) гарантированно приводило бы к аварии при ррˆ, равном nil. Надо сказать, что оператора break в оригинальном Паскале тоже не было. В ситуациях, аналогичных нашей, приходилось вводить дополнительную логическую переменную и обвешивать тело цикла if’ами. Впрочем, в оригинальном Паскале не было и операции взятия адреса, так что применить нашу технику “указатель на указатель” мы бы там не смогли.

Free Pascal позволяет задействовать “классическую” семантику вычисления логических выражений, когда все подвыражения обязательно вычисляются. Это включается директивой {$В+}, а выключается директивой {$В-}. К счастью, по умолчанию используется именно режим {$В-}. Скорее всего, вам в вашей практике никогда не потребуется этот режим менять; если вам кажется, что такая потребность возникла, подумайте ещё.

2.13.7. Двусвязные списки; деки

Списки, которые мы рассматривали до сих пор, называются односвязными, что очевидным образом наводит на мысль о существовании каких-то других списков. В этом параграфе мы рассмотрим списки, называемые двусвязными.

Вводя понятие односвязного списка, мы отметили, что это название с одинаковым успехом можно объяснить наличием только одного указателя, указывающего на каждый из элементов списка; наличием в каждом элементе только одного указателя для поддержания связности; и наличием в списке только одной связной цепочки, выстроенной из указателей. Подобно этому, в двусвязном списке на каждый элемент списка указывает два указателя (из предыдущего элемента и из следующего), каждый элемент имеет два указателя — на предыдущий элемент и на следующий, и в списке присутствуют две цепочки связности — прямая и обратная. Следует отметить, что обычно (хотя и не всегда) с таким списком работают с помощью двух указателей — на первый его элемент и на последний. Пример двусвязного списка показан на рис. 2.12.

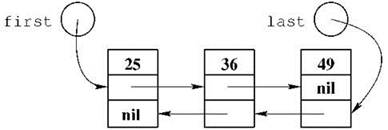
Рис. 2.12. Двусвязный список из трёх элементов

Построить двусвязный список можно из звеньев, описанных, например, так:

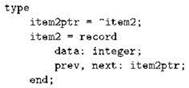
Как и в случае со словом next для указателя на следующий элемент, слово prev (от англ. previous) традиционно обозначает указатель на предыдущий; конечно, вам никто не мешает использовать другое название, но если вашу программу будет читать кто-то ещё, то понять её окажется сложнее.

Надо сказать, что двусвязные списки применяются несколько реже, чем односвязные, поскольку требуют вдвое больше действий с указателями при любых операциях вставки и удаления звеньев, да и сами звенья за счёт наличия двух указателей вместо одного становятся больше, т. е. занимают больше памяти. С другой стороны, у двусвязных списков имеется целый ряд несомненных достоинств в сравнении с односвязными. Прежде всего это очевидная симметрия, которая позволяет просматривать список как в прямом направлении, так и в обратном; в некоторых задачах это оказывается важно.

Второе несомненное достоинство двусвязного списка не столь очевидно, но иногда оказывается даже важнее: зная адрес любого из звеньев двусвязного списка, мы можем найти в памяти все его звенья. Между прочим, при работе с двусвязным списком никогда не требуется рассмотренная в предыдущем параграфе техника с использованием указателя на указатель. В самом деле, пусть на текущее звено указывает некий указатель current; если в текущем звене поле prev нулевое, то, значит, это первое звено и при вставке нового элемента слева от него требуется изменить first; в противном случае звено не первое, то есть имеется предыдущее, в котором нужно изменить поле next, но ведь мы знаем, где оно находится: выражение currentˆ.prevˆ.next как раз даёт тот указатель, который надо будет изменить. Кроме того, нужно будет изменить поле currentˆ.prev. Аналогично производится и вставка справа от текущего звена: сначала нужно поменять currentˆ.nextˆ.prev, а если его нет (то есть текущее звено — последнее в списке), то last; затем меняется currentˆ.next.

Если на первое, последнее и текущее звенья двусвязного списка указывают соответственно указатели first, last и current, новое число находится в переменной n, а временный указатель называется tmp, вставка нового звена слева от текущего выглядит так:

Вставка справа выглядит аналогично:

Удаление текущего элемента делается и того проще:

Этот фрагмент обладает некоторым недостатком: указатель current после его выполнения указывает на несуществующий (уничтоженный) элемент. Этого можно избежать, если воспользоваться временным указателем для удаления элемента, а в current предварительно (до уничтожения текущего элемента) занести адрес предыдущего или следующего, в зависимости от того, проходим мы список в прямом направлении или в обратном.

Добавление элемента в начало двусвязного списка с учётом возможного особого случая может выглядеть, например, так:

Добавление в конец производится аналогично (с точностью до замены направления):

Можно обобщить вышеприведённую процедуру вставки слева от текущего звена, предположив, что если текущего нет (то есть вставка происходит “слева от несуществующего звена”), то это вставка в конец списка. Выглядеть это будет так:

Аналогичное обобщение вставки справа от текущего звена на ситуацию “вставка справа от несуществующего есть вставка в начало” происходит практически так же, меняются только строки, отвечающие за заполнение полей tmpˆ.prev и tmpˆ.next (в нашем фрагменте это строки со второй по шестую):

Схематические диаграммы изменения указателей для всех этих случаев мы не приводим, оставляя визуализацию происходящего читателю в качестве очень полезного упражнения.

Двусвязные списки позволяют создать объект, обычно называемый декой (англ. deque⁴³). Дека — это абстрактный объект, поддерживающий четыре операции: добавление в начало, добавление в конец, извлечение из начала и извлечение из конца. Значение, добавленное в начало деки, можно сразу же извлечь обратно (применив извлечение из начала), но если извлекать значения из конца, то значение, только что добавленное в начало, будет извлечено после всех остальных значений, хранившихся в деке; с добавлением в конец и извлечением из начала ситуация симметричная.

При использовании только операций “добавление в начало” и “извлечение из начала” дека превращается в стек (как, впрочем, и при использовании добавления и извлечения из конца), а при использовании “добавления в начало” и “извлечения из конца” — в очередь; но использовать деку в качестве стека или обычной очереди не стоит, ведь для стека и очереди возможны гораздо более простые реализации: их можно реализовать через односвязный список, тогда как деку односвязным списком реализовать нельзя (точнее, можно использовать два таких списка, но это очень неудобно).

Отметим, что по-английски соответствующие операции обычно называются pushfront, pushback, popfront и popback.

Начать реализацию деки можно, как обычно, с заглушки. К примеру, для деки, хранящей числа типа longint, заглушка будет такая:

Реализовать все эти процедуры и функции мы предложим читателю самостоятельно.

2.13.8. Обзор других динамических структур данных

Прежде всего отметим, что во многих задачах звено списка содержит не одно поле данных, как в наших примерах, а несколько таких полей. Часто возникает потребность связать одно значение с другими, например, инвентарный номер с описанием предмета, или имя человека с его подробной анкетой, или сетевой адрес компьютера с описанием работающих на нём сетевых служб и т. п. В этом случае в одном звене размещают как ту информацию, по которой происходит поиск (номер, имя, адрес), так и те данные, которые служат результатом поиска. Отметим, что информацию, по которой проводится поиск, называют ключом поиска.

Поиск нужной информации в списке — неважно, односвязный он или двусвязный — происходит достаточно медленно, ведь список приходится просматривать звено за звеном, пока не будет найден нужный ключ. Даже если список поддерживается в отсортированном по ключу порядке, в среднем приходится на каждый поиск просмотреть половину звеньев списка. Иначе говоря, в среднем при поиске записи с нужным ключом в списке на каждый поиск тратится kn операций, где n — длина списка, а k — некий постоянный коэффициент; иначе говоря, длительность каждой операции поиска линейно зависит от количества хранящихся записей. Если, скажем, длина списка возрастёт втрое, то во столько же раз возрастёт среднее время, затрачиваемое на поиск нужной записи. Такой поиск так и называют линейным.

Линейный поиск может удовлетворить нас только в задачах, где количество записей не превышает нескольких десятков; если записей будет несколько сотен, с линейным поиском начнутся проблемы; при нескольких тысячах записей пользователь может возмутиться тем. насколько медленно работает наша программа, и будет прав; ну а когда счёт записей переходит в область десятков тысяч, про линейный поиск следует забыть — с таким же успехом мы могли бы вовсе не писать программу, всё равно она окажется бесполезной.

К счастью, многообразие структур данных, построенных из звеньев, плавающих в “куче”, никоим образом не исчерпывается списками. Резко сократить время поиска позволяют более “хитрые” структуры данных; один из самых простых вариантов здесь — так называемое двоичное дерево поиска. Как и список, дерево строится из переменных типа “запись”, содержащих поля-указатели на запись того же типа; записи, составляющие дерево, обычно называют узлами. В простейшем случае каждый узел имеет два поля-указателя — на правое поддерево и на левое поддерево; обычно их называют left и right. Указатель, содержащий значение nil, рассматривается как пустое поддерево.

Двоичное дерево поиска поддерживается в отсортированном виде; в данном случае это означает, что как для самого дерева, так и для любого его поддерева все значения, которые меньше значения в текущем узле, располагаются в левом поддереве, а все значения, большие текущего — в правом. Пример двоичного дерева поиска, содержащего целые числа, приведён на рис. 2.13. В таком дереве найти любой элемент, зная нужное значение, либо убедиться, что такого элемента в дереве нет, можно за число действий, пропорциональных высоте дерева, то есть длине наибольшей возможной связной цепочки от корня дерева до “листового” узла (в дереве на рисунке такая высота составляет три). Отметим, что двоичное дерево высотой h может содержать до 2^h — 1 узлов; например, в дерево высотой 20 можно поместить свыше миллиона значений, при этом поиск будет происходить за 20 сравнений; если бы те же значения находились в списке, то сравнений на каждый поиск в среднем требовалось бы полмиллиона.

Рис. 2.13. Двоичное дерево поиска, хранящее целые числа

Конечно, при ближайшем рассмотрении всё оказывается не столь просто и радужно. Дерево далеко не всегда так плотно заполняется узлами, как на нашем рисунке. Пример такой ситуации приведён на рис. 2.14; при высоте 5 дерево здесь содержит всего девять узлов из 31 возможных. Такое дерево называется разбалансированным. В наихудшем случае дерево вообще может принять вырожденную форму, когда его высота будет равна количеству элементов; это происходит, например, если значения, вносимые в дерево, исходно расположены по возрастанию или по убыванию. Впрочем, то, что для дерева представляет собой наихудший вариант, для списка происходит всегда. Кроме того, существуют алгоритмы балансировки деревьев, позволяющие перестроить дерево поиска, уменьшив его высоту до минимально возможной; эти алгоритмы достаточно сложны, но реализовать их можно.

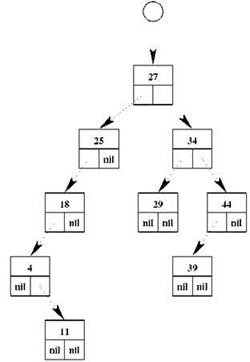
Рис. 2.14. Разбалансированное двоичное дерево поиска

К рассмотрению двоичных деревьев поиска мы вернёмся в главе, посвящённой “продвинутым” случаям использования рекурсии. Дело в том, что все основные операции над двоичным деревом, кроме разве что балансировки, многократно (!) проще записать с помощью рекурсии, чем без неё. Пока же отметим, что деревья, разумеется, бывают не только двоичными; в общем случае количество потомков у узла дерева можно сделать сколь угодно большим или вообще динамически изменяемым. Например, широко известен способ хранения текстовых строк, при котором каждый узел дерева может иметь столько потомков, сколько есть букв в алфавите; при поиске выбор потомка очередного узла производится в соответствии с очередной буквой в строке. Высота такого дерева строго равна длине самой длинной из хранящихся в нём строк, а в балансировке оно не нуждается.

Время поиска в списке пропорционально длине списка, время поиска в сбалансированном двоичном дереве, как можно догадаться, пропорционально двоичному логарифму от количества узлов; для случаев, когда время поиска критично, а объём хранимых данных велик, известен подход, при котором время поиска вообще не зависит от количества хранимых элементов — оно сохраняется постоянным хоть для десятка значений, хоть для десяти миллионов. Метод носит название хеш-таблицы.

Для создания хеш-таблицы используют так называемую хеш-функцию. В принципе, это просто некая арифметическая функция, которая по заданному значению ключа поиска выдаёт некое целое число, причём это число должно быть трудно предугадать; говорят, что хеш-функция должна представлять собой хорошо распределённую случайную величину. При этом важно, что хеш-функция должна зависеть только от значения ключа, то есть на одних и тех же ключах хеш-функция должна всегда принимать одни и те же значения. Сама хеш-таблица представляет собой массив размера, заведомо превосходящего нужное количество записей; изначально все элементы массива помечаются как свободные. Вычислив хеш-функцию, по её значению определяют, в какой позиции массива должна находиться запись с заданным ключом; это делают, попросту вычислив остаток от деления значения хеш-функции на длину массива. Чтобы снизить вероятность попаданий двух ключей в одну позицию, размер массива, используемого для таблицы, обычно выбирают равным простому⁴⁴ числу.

Если при занесении нового элемента в хеш-таблицу вычисленная позиция оказалась пуста, новую запись заносят в эту позицию. Если при поиске ключа в хеш-таблице вычисленная позиция оказалась пуста, считается, что записи с таким ключом в таблице нет. Несколько интереснее вопрос о том, что делать, если позиция занята, но ключ записи в этой позиции отличается от ключа, который нам нужен; такая ситуация означает, что у двух разных ключей, несмотря на все наши старания, оказались одинаковые остатки от деления хеш-функции на длину массива. Это называется коллизией. Основных методов разрешения коллизии известно два. Первый из них очень простой: в массиве хранятся не сами записи, а указатели, позволяющие сформировать список (обычный односвязный) из записей, ключи которых дают одно и то же значение хеша (точнее, не хеша, а его остатка от деления на длину массива). Способ, при его внешней простоте, имеет очень серьёзный недостаток: списки сами по себе достаточно громоздки, работа с ними отнимает много времени.

Второй способ разрешения коллизий выглядит хитрее: если позиция в таблице занята записью, ключ которой не совпадает с искомым, используют следующую позицию, а если и она занята, то следующую за ней, и так далее. При занесении в таблицу новой записи её просто помещают в первую же найденную (после определённой с помощью хеш- функции) свободную позицию; при поиске просматривают записи одну за другой в поисках нужного ключа, и если при этом натыкаются на свободную запись, считается, что искомый ключ в таблице отсутствует. К недостаткам этого метода относится довольно неочевидный алгоритм удаления записи из таблицы. Проще всего поступить так: если позиции, непосредственно следующие за удаляемой записью, чем-то заняты, то найти первую свободную позицию таблицы, а затем последовательно каждую запись, расположенную в таблице между только что удалённой и найденной первой свободной, временно удалить из таблицы, а затем включить обратно по обычному правилу (при этом запись может оказаться включённой раньше либо в точности в том же месте). Ясно, что времени на это может уйти довольно много. В литературе можно найти более эффективные процедуры удаления записей, которые при этом существенно сложнее объяснить и, как следствие, можно сделать ошибку при реализации, обусловленную непониманием описания алгоритма.

Надо сказать, что оба способа (первый в меньшей степени, второй в большей) чувствительны к заполнению таблицы. Считается, что хеш- таблица должна быть заполнена не более чем на две трети, в противном случае постоянно производимый линейный поиск (по спискам либо по самой таблице) сведёт на нет все преимущества хеширования. Если записей в таблице стало слишком много, её необходимо перестроить с использованием нового размера; например, можно увеличить текущий размер вдвое, после чего найти ближайшее сверху простое число и объявить новым размером таблицы. Перестроение таблицы — операция крайне неэффективная, ведь каждую запись из старой таблицы придётся внести в новую по обычному правилу с вычислением хеш-функции и взятием остатка от деления, и никаких “сокращённых” алгоритмов для этого нет.

Так или иначе, можно заметить, что для построения хеш-таблиц нужны массивы с заранее неизвестной — динамически определяемой — длиной. В оригинальный язык Паскаль такие средства не входили; современные диалекты, включая Free Pascal, поддерживают динамические массивы, но рассматривать их мы не будем; при желании вы можете освоить этот инструмент самостоятельно.