Весь курс начальной школы в схемах и таблицах 1-4 классы - 2015 год
Задачи на встречное движение - МАТЕМАТИКА
Если два тела одновременно движутся навстречу друг другу, то расстояние между ними постоянно изменяется на одно и то же число, равное сумме расстояний, которые проходят тела за единицу времени.
Два лыжника одновременно вышли навстречу друг другу из двух посёлков и встретились через 3 ч. Первый лыжник шёл со скоростью 12 км/ч, а второй — 14 км/ч. На каком расстоянии находятся посёлки?
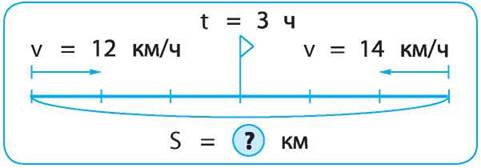
Схема анализа задачи:
1-й способ
— О чём говорится в задаче?
— О движении двух лыжников. Поэтому краткое условие к задаче оформляем в виде рисунка.
— Что известно о начале движения?
— Лыжники начали двигаться одновременно. Покажем это стрелочками “навстречу”.
Выводы:
1. Расстояние между лыжниками всё время уменьшается.
2. Всё расстояние складывается из расстояния, которое прошёл первый лыжник, и расстояния, которое прошёл второй лыжник.
3. Лыжники начали и закончили движение одновременно, поэтому они провели в пути одинаковое количество времени.
Решаем задачу, опираясь на схему:
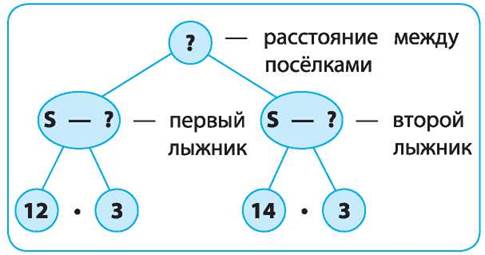
Решение.
1) 12 · 3 = 36 (км) — прошёл первый лыжник до встречи
2) 14 · 3 = 42 (км) — прошёл второй лыжник до встречи
3) 36 + 42 = 78 (км) — расстояние между посёлками.
Выражение: 12 · 3 + 14 · 3 = 78 (км)
Ответ: расстояние между посёлками — 78 км.
2-й способ
Решим эту задачу, используя понятие “скорость сближения”.
Если первый лыжник пройдёт за 1 час 12 км, а второй — 14 км, то расстояние между ними за 1 час уменьшится (это и есть скорость сближения) на: 12 + 14 = 26 км. За второй час расстояние уменьшится ещё на 26 км.
Решение.
1) 12 + 14 = 26 (км/ч) — скорость сближения;
2) 26 · 3 = 78 (км).
Выражение: (12 + 14) · 3 = 78 (км).
Ответ: расстояние — 78 км.