ФИЗИКА + МАТЕМАТИКА = ЛОГИКА - 9 класс

Тип урока: урок-соревнование.

Интеграция предметов: физика — математика.

Правила соревнования:

1. Интегративное соревнование требует хороших знаний по физике и математике и логического мышления.

2. Набирается группа сильных учащихся в количестве 10 человек. Между ними и проходят соревнования на приз «Эрудит».

3. Кто из учащихся набирает большее число «плюсов», тот и выходит в лидеры.

4. Если ни один из участников соревнования не может ответить на вопрос, то ответ могут дать болельщики.

5. Соревнования проходят в 4 этапа.

Ход урока

Ведущий. «Отыщи всему начало, и ты многое поймешь», — говорил Козьма Прутков. А всему начало в нашем соревновании, по-моему, ваше желание, ваше стремление, ваш ум.

Начинаем соревнование за приз «Эрудит»!

Ведущий. Первым этапом нашего соревнования является «Физико-математическая лесенка». (Вопросы лесенки зачитываются ведущим.)

Математическая лесенка

1. Как увеличить число 666 в полтора раза, не прибегая к помощи арифметики?

Ответ. Надо 666 поделить пополам, будет 333, а затем 666 + 333 = 999.

2. Что дороже: полкилограмма двугривенных или килограмм гривенников?

Ответ. Одинаково.

3. Сколько нужно считать, чтобы дойти от единицы до миллиарда при скорости счета — одно число в секунду?

Ответ. Около 32 лет (1 сут. = 24 ч = 24 · 3600 с = 86 400 с;

Физическая лесенка

1. Стоя на движущемся эскалаторе, вы выбираетесь на поверхность за 1 мин; если бы вы бегом поднимались по неподвижному эскалатору, то это заняло бы 40 с. За сколько времени вы взбежите наверх по движущемуся эскалатору?

Ответ. За 20 с.

2. При какой скорости движения собаки не будет слышен звук от ударов о мостовую сковородки, привязанной к ее хвосту.

Ответ. Если собака бежит со скоростью звука ≈ 330 м/с.

3. Лучший прыгун на Земле преодолевает высоту 2,1 м. Как высоко он прыгал бы на Луне, где сила тяжести в 6 раз меньше? Рост прыгуна 1,8 м.

Отчет. На 7,2 м. (Свой центр тяжести он поднимает на Земле только на 1,2 м , значит на Луне 1,2 · 6 = 7,2 м.)

Ведущий. Второй этап наших соревнований называется «Физико-математический эксперимент». А заключается он в следующем.

1. Как положить находящийся на столе шарик в банку, не прикасаясь к нему руками и не подкатывая его к краю стола?

Ответ. Накрывать шарик банкой, круговыми движениями заставить его кататься по стенкам банки, а затем быстро повернуть банку дном вниз.

2. Как найти центр тяжести учительской указки?

Ответ. На указательные пальцы расставленных рук положите гладкую указку. Теперь двигайте пальцы навстречу друг другу, пока они не сойдутся вплотную. Пальцы сошлись под центром тяжести.

Ведущий. Следующий этап наших состязаний требует пространственного воображения, логического мышления и хорошего знания точных наук.

Физико-математические задачи в рисунках и чертежах

1. Перед вами «снимок» глади озера сверху. Точки «А» и «М» — пловцы, окружности — волны. Куда плывут пловцы? Какой из пловцов плывет быстрее? Какова скорость пловцов, если скорость волн 0,5 м/с?

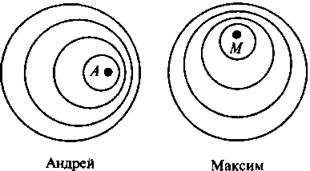
Ответ. Центры всех окружностей — последовательное положение пловцов. О1 — центр самой большой окружности, т.е. место старта пловца. Следовательно, пловец А плывет вправо, пловец М — вперед (вверх) О1А > О1М, значит скорость пловца А больше. Расстояние O1B > О1А в 2 раза, следовательно, скорость пловца А вдвое меньше скорости волн VA = 0,25 м/с.

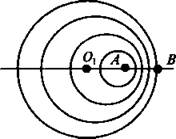
Скорость пловца М еще меньше VM = 0,125 м/с, т. к. О1М < О1А в 2 раза.

2. Найдите центр тяжести фигуры, изображенной на рисунке.

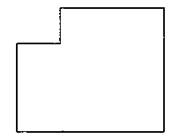
Ответ. Разбиваем фигуру на два прямоугольника, а центры тяжести данных прямоугольников лежат на пересечении диагоналей.

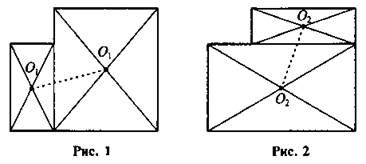
При совмещении рисунков 1 и 2 на пересечении прямых О1О1 и О2О2 мы получим центр тяжести фигуры. Центр тяжести фигуры — точка О.

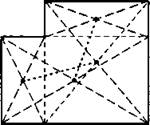
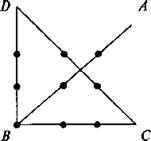
3) Соедините все девять точек, не отрывая руки от чертежа, только четырьмя прямыми линиями.

Ответ. Четыре линии надо провести так, как показано на рисунке ABCDB (стрелка).

Ведущий. Последним этапом нашего интеллектуального состязания будет задача, которая так и называется, — «Эрудит». Послушаем ее условие. Вы должны произвести теоретические расчеты, а экспериментально вы можете ее проверить дома.

Представьте себе, что перед вами мяч диаметром 12,5 см, обтянутый по окружности плотно прилегающей к нему веревкой. На сколько отойдет веревка от поверхности мяча по всей окружности, если веревку удлинить на 10 см.

Ответ. Начальная длина веревки была т. е. длина окружности мяча. При удлинении веревка станет 49,25 см, тогда диаметр (радиус) воображаемой окружности станет:

Определим разность диаметров и результат поделим на 2:

Ведущий. Наше интеллектуальное состязание подошло к концу. Спасибо! «Только хорошо зная чужое, можно создать что-то свое, принципиально новое». И я пожелаю вам терпения, трудолюбия и удачи!

(Награждение победителя).