Уроки геометрии в задачах 7—8 классы - М. А. Волчкевич 2016
Угол между касательной и хордой
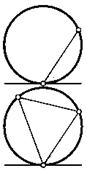
Теорема. Угол между касательной и хордой окружности, проведенными в одной ее точке, равен половине градусной меры дуги окружности, находящейся внутри этого угла.
Из теоремы сразу следует, что угол между касательной и хордой равен вписанному в эту окружность углу, опирающемуся на указанную дугу.
L Докажите, что отрезок, соединяющий основания двух высот треугольника, параллелен касательной к его описанной окружности, проведенной в вершине треугольника.
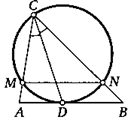
2. Через концы биссектрисы CD треугольника АВС провели окружность, которая касается стороны АВ в точке D и пересекает другие его стороны в точках М и N. Докажите, что отрезок MN параллелен стороне АВ.
3. Две окружности пересекаются в точках Л и Б. На одной из них взяли произвольную точку М. Прямые МА и МВ вторично пересекают другую окружность в точках Р и Q. Докажите, что прямая PQ параллельна касательной к первой окружности, проведенной в точке М.
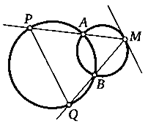
4. Через точку касания двух окружностей проводят две произвольные прямые, пересекающие первую окружность в точках А и В, а вторую —в точках С и D. Докажите, что прямые АВ и CD параллельны. Разберите также случай внутреннего касания.
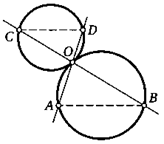
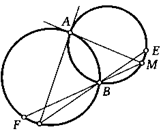
5. Две окружности пересекаются в точках А и В. Через точку В провели прямую, которая вторично пересекла данные окружности в точках Ми К. В этих точках к окружностям провели касательные, которые пересеклись в точке Е. Докажите, что точки А, М, Е, К всегда лежат на одной окружности.
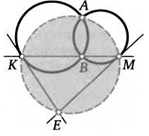
6. В треугольнике АВС провели высоты AM и СК. Через точки В, К и М провели окружность. Докажите, что касательные к этой окружности, проведенные в точках М и К, пересекаются на стороне АС.
В
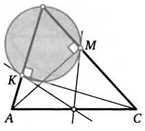
7. Две окружности пересекаются в точках Л и В. В точке А к ним провели касательные, которые пересекают эти окружности в точках М и К. Прямые ВМ и КМ вторично пересекают данные окружности в точках Е и F. Докажите, что FM = EK.
К
8. Вписанная в треугольник АВС окружность касается его стороны АС в точке М, а двух других его сторон в точках Е и К. Докажите, что отрезок АС виден из середин отрезков ME и МК под одинаковым углом.
В
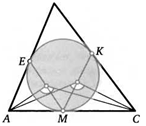
К задаче 8
9. Из точки М к окружности проведены касательные МА и МВ. Еще одна окружность проходит через точки М и А и касается прямой АВ. Пусть Е — точка пересечения данных окружностей, отличная от А. Докажите, что прямая BE делит отрезок AM пополам.
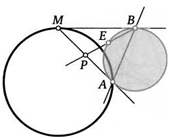
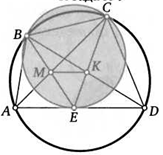
10. Четырехугольник ABCD вписан в окружность. Другая окружность проходит через точки В и С и касается стороны AD в точке Е. Отрезки BE и СЕ пересекают диагонали четырехугольника в точках М и К. Докажите, что прямая МК параллельна AD.